题目内容
下图是一个几何体的三视图，根据图中数据，可得该几何体的表面积为（ ）.
A． | B． | C． | D． |
D
解析考点：由三视图求面积、体积．
分析：由题意可知，几何体是由一个球和一个圆柱组合而成的，依次求表面积即可．
解：从三视图可以看出该几何体是由一个球和一个圆柱组合而成的，其表面为S=4π×12+π×12×2+2π×1×3=12π
故选D．
练习册系列答案
相关题目
如图是一个几何体的三视图，若它的体积是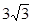
，则图中主视图所标
=
| A．1 | B． | C． | D． |
一个平面截一个球得到截面面积为
的圆面，球心到这个平面的距离是
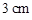，则该球的表面积是（ ）
| A． | B． | C． | D． |
如图，平行四边形ABCD中，
沿BD将
折起，使面
面
，连结AC，则在四面体ABCD的四个面中，互相垂直的平面共有（ ）对
| A．1 | B．2 | C．3 | D．4 |
已知下列四个命题：①平行于同一直线的两平面互相平行；②平行
于同一平面的两平面互相平行；
③垂直于同一直线的两平面互相平行；④与同一直线成等角的两条直线互相平行。
其中正确命题是（ ）
| A．①② | B．②③ | C．③④ | D．②③④ |
有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2，且该塔形的表面积(含最底层正方体的底面面积)超过39，则该塔形中正方体的个数至少是
| A．4 | B．5 | C．6 | D．7 |
如图长方体中，
，
，则二面角
的大小为（ ）
A． | B． | C． | D． |
已知正方体的外接球的体积是
，则这个正方体的棱长是
A． | B． | C． | D． |