题目内容
 已知三角函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<
已知三角函数f(x)=Acos(ωx+φ)+B(A>0,ω>0,|φ|<| π |
| 2 |
(Ⅰ)求函数的解析式;
(Ⅱ)将函数f(x)的图象向右平移
| π |
| 6 |
分析:(I)根据函数图象求出A,T,求出ω,利用点(
,-1)在曲线上,求出φ,看出图象向上平移的大小,得到解析式.
(II)根据将函数f(x)的图象向右平移
个单位后得到函数g(x)的解析式,根据余弦函数的单调区间得到范围,解出x的范围.
| π |
| 3 |
(II)根据将函数f(x)的图象向右平移
| π |
| 6 |
解答:解:(Ⅰ)由题知A+b=3,-A+b=-1,
=
-(-
)=
,…(2分)
所以A=2,b=1,w=2,又f(
)=-1得?=
,…(4分)
所以函数的解析式为:f(x)=2cos(2x+
)+1.…(6分)
(Ⅱ)由题意得:g(x)=2cos2x+1,…(8分)
所以g(x)在[kπ-
,kπ]k∈z递增,…(10分)
在[kπ,kπ+
]k∈z递减…(12分)
| T |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
所以A=2,b=1,w=2,又f(
| π |
| 3 |
| π |
| 3 |
所以函数的解析式为:f(x)=2cos(2x+
| π |
| 3 |
(Ⅱ)由题意得:g(x)=2cos2x+1,…(8分)
所以g(x)在[kπ-
| π |
| 2 |
在[kπ,kπ+
| π |
| 2 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,学会读图,选择适当的点的坐标,能够简化计算过程,这是一个典型的三角函数问题.

练习册系列答案
相关题目
已知三角函数f(x)=sin2x-cos2x,其中x为任意的实数.求此函数的周期为( )
| A、2π | B、π | C、4π | D、-π |
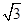 sin(ωx+φ)
(0<φ<π,ω>0)过点
sin(ωx+φ)
(0<φ<π,ω>0)过点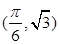 ,函数y=f(x)图象的两相邻对称轴间的距离为
,函数y=f(x)图象的两相邻对称轴间的距离为 .
.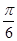 个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
个单位后,得到函数y=g(x)的图象,求函数g(x)的单调递减区间. ,
, 所以
所以


 ,
,  可以得到单调区间。
可以得到单调区间。 ,得
,得 …………1分
…………1分 ,
,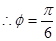 ∴
∴
 的单调递减区间为
的单调递减区间为 ,
, .
.