题目内容
已知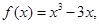 过点
过点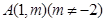 可作曲线
可作曲线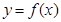 的三条切线,则
的三条切线,则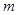 的取值范围是
的取值范围是
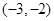
解析试题分析:设切点为(t,t³-3t),因为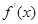 =3x²-3,
=3x²-3,
则切线方程为y=(3t²-3)(x-t)+t³-3t
整理得y=(3t²-3)x-2t³
把A(1,m)代入整理得:2t³-3t²+m+3=0 ①
因为可作三条切线,所以①有三个解
记g(t)=2t³-3t²+m+3
则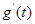 =6t²-6t=6t(t-1)
=6t²-6t=6t(t-1)
所以当t=0时,极大值g(0)=m+3,
当t=1时,极小值g(1)=m+2
要使g(t)有三个零点,只需m+3>0且m+2<0,解得-3<m<-2,
故答案为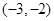 。
。
考点:本题主要考查导数的几何意义。
点评:基础题,过曲线上点的切线斜率,就是函数在该点的导数值。

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
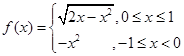 ,则函数
,则函数 图像与直线
图像与直线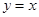 围成的封闭图形的面积是__________。
围成的封闭图形的面积是__________。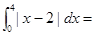 _________
_________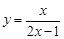 在点
在点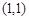 处的切线方程为 .
处的切线方程为 .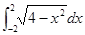 =___________
=___________ 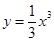 上的点
上的点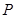 的切线
的切线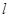 的方程为
的方程为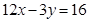 ,那么
,那么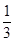 x3+2与曲线y=4x2-1在x=x0处的切线互相垂直,则x0的值为
x3+2与曲线y=4x2-1在x=x0处的切线互相垂直,则x0的值为 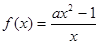 的单调增区间为(0,+∞),则实数
的单调增区间为(0,+∞),则实数 的取值范围是________.
的取值范围是________.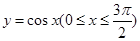 与坐标轴围成的面积是 .
与坐标轴围成的面积是 .