题目内容
某校高三年级一次数学考试之后,为了解学生的数学学习情况, 随机抽取
名学生的数学成绩, 制成下表所示的频率分布表．
(1)求
，
，的值;
(2)若从第三, 四, 五组中用分层抽样方法抽取6名学生，并在这6名学生中随机抽取2名与张老师面谈，求第三组中至少有
名学生与张老师面谈的概率．
名学生的数学成绩, 制成下表所示的频率分布表．(1)求
，，的值;(2)若从第三, 四, 五组中用分层抽样方法抽取6名学生，并在这6名学生中随机抽取2名与张老师面谈，求第三组中至少有
名学生与张老师面谈的概率．| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  |  |  |
| 第二组 |  | |  |
| 第三组 |  |  |  |
| 第四组 |  |  | |
| 第五组 |  |  |  |
| 合计 | |  | |
(1)
，
，
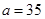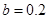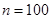；(2)0．8．
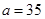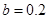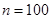，，；(2)0．8．试题分析：(1)先由频数与频率及n的关系：
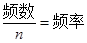，任选一组已知了频数和频率的就可求出n的值，进而再利用这个关系式就可求出a,b的值；(2)首先利用分层抽样：即各层按相同比例
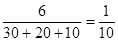计算出各组中应抽取的样本数，显然第三、四、五组分别抽取3、2、1名学生，并将这六名学生用不同的字母来表示，然后用树图写出从中任抽两名的所有不同的取法，数出总数并数出第三组中的三名学生没有人抽取的种数，从而就可求出第三组中没有人与张老师面谈的事件的概率
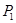，由于第三组中至少有名学生与张老师面谈的事件与第三组中没有人与 张老师面谈的事件是对立事件，所以所求概率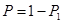
．试题解析：(1)依题意，得
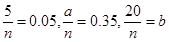，解得，
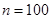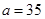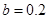，，． 3分(2)因为第三、四、五组共有60名学生，用分层抽样方法抽取6名学生，
则第三、四、五组分别抽取
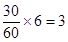名，
名，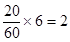
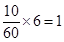名． 6分第三组的
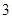名学生记为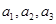
，第四组的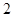
名学生记为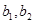
，第五组的名学生记为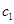
，则从
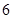名学生中随机抽取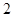名，共有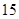
种不同取法，具体如下：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
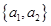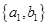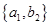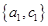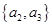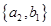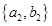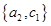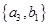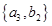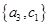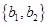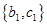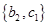． 8分其中第三组的
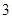名学生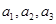没有一名学生被抽取的情况共有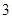种，具体如下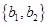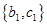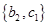：，，． 10分故第三组中至少有
名学生与张老师面谈的概率为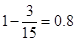
． 12分
练习册系列答案
名校课堂系列答案
相关题目
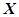为取得红球的个数．
；
；
；
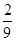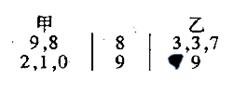
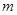个红球和
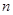个篮球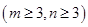
，从乙盒中随机抽取
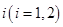个球放入甲盒中.
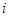个球后，甲盒中含有红球的个数记为
；
.
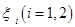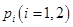