题目内容
(本题14分)设函数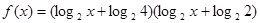 的定义域为
的定义域为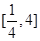 ,
,
(Ⅰ)若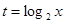 ,求
,求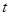 的取值范围;
的取值范围;
(Ⅱ)求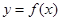 的最大值与最小值,并求出最值时对应的
的最大值与最小值,并求出最值时对应的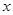 的值.
的值.
【答案】
(Ⅰ)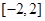
(Ⅱ)当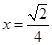 时,
时,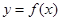 有最小值
有最小值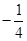 ;当
;当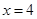 时,
时,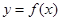 有最大值
有最大值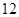 .
.
【解析】
试题分析:(Ⅰ)因为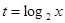 ,而
,而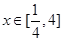 ,
,
所以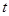 的取值范围为区间
的取值范围为区间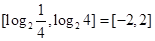 . ……6分
. ……6分
(Ⅱ)记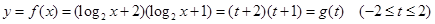 .……7分
.……7分
∵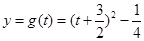 在区间
在区间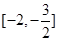 是减函数,在区间
是减函数,在区间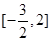 是增函数, ……8分∴当
是增函数, ……8分∴当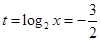 即
即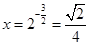 时,
时,
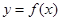 有最小值
有最小值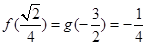 ; ……11分
; ……11分
当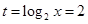 即
即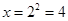 时,
时,
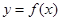 有最大值
有最大值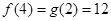 . ……14分
. ……14分
考点:本小题主要考查换元法的应用和二次函数在闭区间上的最值问题,考查学生的运算求解能力.
点评:换元法经常考查应用,要特别注意换元前后变量的范围是否发生了变化.

练习册系列答案
相关题目
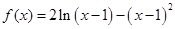 .
.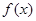 的单调递增区间;
的单调递增区间;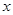 的方程
的方程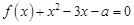 在区间
在区间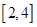 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数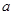 的取值范围.
的取值范围.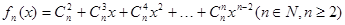 ,当
,当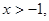 且
且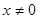 时,证明:
时,证明: 恒成立
恒成立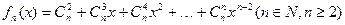 ,当
,当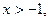 且
且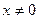 时,证明:
时,证明: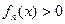 恒成立
恒成立