题目内容
已知函数 是定义在R上的奇函数,且
是定义在R上的奇函数,且 ,在[0,2]上
,在[0,2]上 是增函数,则下列结论:①若
是增函数,则下列结论:①若 ,则
,则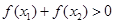 ;②若
;②若 且
且 ③若方程
③若方程 在[-8,8]内恰有四个不同的角
在[-8,8]内恰有四个不同的角 ,则
,则 ,其中正确的有 ( )
,其中正确的有 ( )
| A.0个 | B.1个 | C.2个 | D.3个 |
D
解析解:由f(x+4)=-f(x)可得f(x+8)=f(x),此函数是以8为周期的周期函数,
又f(x)是奇函数,且在[0,2]上为增函数
∴f(x)在[-2,0]上也是增函数
当x∈[2,4]时,x-4∈[-2,0],且由已知可得f(x-4)=-f(x),则可得函数f(x)在[2,4]上单调递减,根据奇函数的对称性可知,f(x)在[-4,-2]上也是单调递减
①若0<x1<x2<4,且x1+x2=4,则0<x1<4-x1<4,即0<x1<2,-2<x1-4<0
由f(x)在[0,2]上是增函数可得f(x)在[-2,0]上也是增函数,则f(x1)>f(x1-4)=f(-x2)=-f(x2),则f(x1)+f(x2)>0;故①正确
②若0<x1<x2<4,且x1+x2=5,则0<x1<5-x1<4,即1<x1<5/2,f(x)在[0,2]上是增函数,由图可知:f(x1)>f(x2);故②正确;
③四个交点中两个交点的横坐标之和为2×(-6),另两个交点的横坐标之和为2×2,此时x1+x2+x3+x4=-12+4=-8,故③正确;
故答案为①②③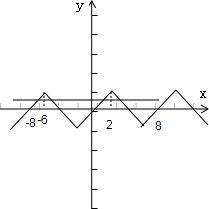

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设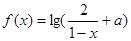 是奇函数,则使
是奇函数,则使 的取值范围是
的取值范围是
| A.(-1,0) | B.(0,1) | C.(- ,0) ,0) | D.(- ,0) ,0) |
函数 的定义域是 ( )
的定义域是 ( )
A. | B. | C. | D. |
已知 y =" f" ( x ) 是定义在R 上的偶函数, 且在( 0 , +  )上是减函数,如果
)上是减函数,如果
x1 < 0 , x2 > 0 ,  且| x1 | < | x2 | , 则有( )
且| x1 | < | x2 | , 则有( )
A. f (-x1 ) + f (-x2 ) > 0 f (-x1 ) + f (-x2 ) > 0 | B.f ( x1 ) + f ( x2 ) < 0 |
| C. f (-x1 ) -f (-x2 ) > 0 | D.f ( x1 ) -f ( x2 ) < 0 |
定义在R上的偶函数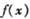 满足
满足 ,当
,当 时
时 ,则
,则
A. | B. |
C. | D. |
若函数 是函数
是函数 的反函数,其图像经过点
的反函数,其图像经过点 ,则
,则 ( )
( )
A. | B. | C.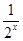 | D. |


 的图象的大致形状是 ( )
的图象的大致形状是 ( )
 ,将函数
,将函数 向左平移
向左平移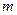 个单位
个单位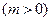 ,所得图象对应的函数为偶函数,则
,所得图象对应的函数为偶函数,则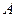 .
.
 .
.
 .
.
 .
.