题目内容
甲盒中装有7个标号为1、2、3、4、5、6、7的小球,乙盒中装有n个标号为1,2,3,…,n的小球,(1)从甲盒中有放回地抽取小球3次,每次抽取一个球,求恰有两次抽取7号球的概率;
(2)现将两盒球均匀混合,从中随机抽取一个小球,若抽取的标号为n的小球的概率为
| 2 | 13 |
分析:(1)有放回地抽取小球3次,每次抽取一个球,恰有两次抽取7号球,这个实验每次取到7号球的概率为
,所以这是一个独立重复试验,根据独立重复试验的公式得到要求的概率.
(2)将两盒球均匀混合后,小球的个数为n+7个,如果n≤7,则n号球有两个,如果n>7,则n号球有1个,根据古典概型公式即可求得n的值.
| 1 |
| 7 |
(2)将两盒球均匀混合后,小球的个数为n+7个,如果n≤7,则n号球有两个,如果n>7,则n号球有1个,根据古典概型公式即可求得n的值.
解答:解:(1)恰有2次抽取7号球的概率为P=C32(
)2•(1-
)=
;
(2)由题意,得:当n≤7时,
=
,
∴n=6.
当n>7时,有
=
,
∴n=-
,不合题意舍去.
∴n=6.
| 1 |
| 7 |
| 1 |
| 7 |
| 18 |
| 343 |
(2)由题意,得:当n≤7时,
| 2 |
| 7+n |
| 2 |
| 13 |
∴n=6.
当n>7时,有
| 1 |
| 7+n |
| 2 |
| 13 |
∴n=-
| 1 |
| 2 |
∴n=6.
点评:本题考查等可能事件的概率,用到的知识点为:概率=所求情况数与总情况数之比,属中档题.

练习册系列答案
相关题目
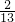 ,求n的值.
,求n的值.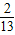 ,求n的值.
,求n的值.