题目内容
如图,F1,F2分别是椭圆![]() +
+![]() =1(a>b>0)的左右焦点,M为椭圆上一点,MF2垂直于x轴,且OM与椭圆长轴和短轴端点的连线AB平行,
=1(a>b>0)的左右焦点,M为椭圆上一点,MF2垂直于x轴,且OM与椭圆长轴和短轴端点的连线AB平行,
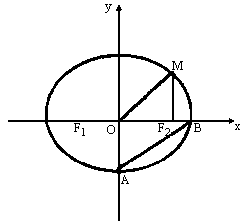
(Ⅰ)求椭圆的离心率;
(Ⅱ)若G为椭圆上不同于长轴端点任一点,求∠F1GF2取值范围;
(Ⅲ)过F2且与OM垂直的直线交椭圆于P,Q.若![]() =20
=20![]() ,求椭圆的方程.
,求椭圆的方程.
答案:
解析:
解析:
|
解:(Ⅰ)由已知M(c, ∵KOM=KAB ∴ (Ⅱ)设GF1=m,GF2=n cosθ= 当且仅当m=n时,(cosθ)min=0 ∴θ∈(0, (Ⅲ) |y1-y2|= ∴c2=b2=25,a2=50 ∴椭圆的方程为 |

练习册系列答案
相关题目
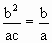 ∴b=c,e=
∴b=c,e=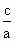 =
=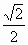
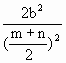 -1=0
-1=0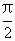 ]
]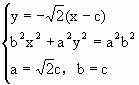
 5y2-
5y2-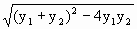 =
=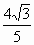 c
c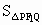 =
=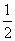 |F1F2||y1-y2|=
|F1F2||y1-y2|=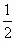 ×2c×
×2c×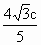 =
=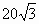
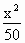 +
+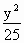 =1
=1 如图,F1,F2分别为椭圆
如图,F1,F2分别为椭圆 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 如图,F1,F2分别为双曲线
如图,F1,F2分别为双曲线 如图,F1、F2分别为椭圆
如图,F1、F2分别为椭圆 的左、右焦点,点P在椭圆上,△POF2是面积
的左、右焦点,点P在椭圆上,△POF2是面积 的正三角形,则
的正三角形,则 的值是
的值是