题目内容
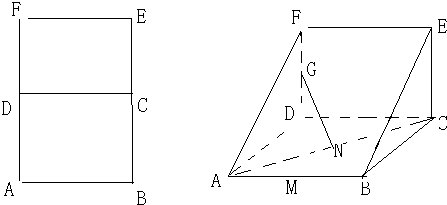 在长方形ABEF中,D,C分别是AF和BE的中点,M和N分别是AB和AC的中点,AF=2AB=2a,将平面DCEF沿着DC折起,使角∠ADF=90°,G是DF上一动点,求证:
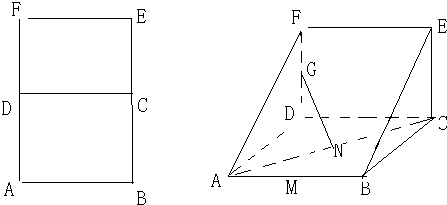
在长方形ABEF中,D,C分别是AF和BE的中点,M和N分别是AB和AC的中点,AF=2AB=2a,将平面DCEF沿着DC折起,使角∠ADF=90°,G是DF上一动点,求证:(1)GN⊥AC
(2)当FG=GD时,在棱AD上确定一点P,使得GP∥平面FMC.并给出证明.
分析:(1)连接BD,结合正方形的几何特征有线面垂直的判定及性质定理,易得AC⊥BD且AC⊥FD,由线面垂直的判定定理可得AC⊥平面BDF,进而根据线面垂直的性质可得GN⊥AC;(2)连接正方形CDFE的对角线DE、CF交于O点,连接OG,GA,OM,由三角形中位线定理及M是AB的中点可得则AM∥OG且AM=OG,进而得到AG∥OM,由线面平行的判定定理,得到:AG∥平面FMC.
解答: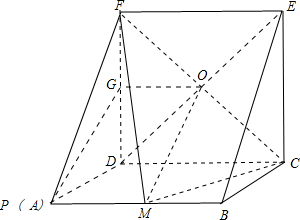
 证明:(1)连接BD,如图所示:
证明:(1)连接BD,如图所示:
∵D,C分别是AF和BE的中点,AF=2AB=2a,
∴四边形ABCD为边长为a的正方形
又∵N为AC的中点,故N为正方形对角线AC与BD的交点
∴AC⊥BD
∵∠ADF=90°
∴FD⊥AD,
又∵FD⊥DC,AD∩CD=D
∴FD⊥平面ABCD
又∵AC?平面ABCD
∴AC⊥FD
∵BD∩FD=D
∴AC⊥平面BDF
∵G∈FD,
∴GN?平面BDF
∴GN⊥AC
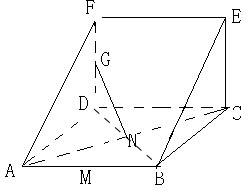
(2)当P点与A点重合时,GP∥平面FMC,理由如下:
∵FG=GD时,G为FD的中点
连接正方形CDFE的对角线DE、CF交于O点,连接OG,GP,OM
则OG∥DC,且OG=
DC,
由PM∥DC,且PM=
DC,
则PM∥OG且PM=OG
则四边形PMOG为平行四边形
则PG∥OM,
又∵PG?平面FMC,OM?平面FMC,
∴PG∥平面FMC

 证明:(1)连接BD,如图所示:
证明:(1)连接BD,如图所示:∵D,C分别是AF和BE的中点,AF=2AB=2a,
∴四边形ABCD为边长为a的正方形
又∵N为AC的中点,故N为正方形对角线AC与BD的交点
∴AC⊥BD
∵∠ADF=90°
∴FD⊥AD,
又∵FD⊥DC,AD∩CD=D
∴FD⊥平面ABCD
又∵AC?平面ABCD
∴AC⊥FD
∵BD∩FD=D
∴AC⊥平面BDF
∵G∈FD,
∴GN?平面BDF
∴GN⊥AC
(2)当P点与A点重合时,GP∥平面FMC,理由如下:
∵FG=GD时,G为FD的中点
连接正方形CDFE的对角线DE、CF交于O点,连接OG,GP,OM
则OG∥DC,且OG=
| 1 |
| 2 |
由PM∥DC,且PM=
| 1 |
| 2 |
则PM∥OG且PM=OG
则四边形PMOG为平行四边形
则PG∥OM,
又∵PG?平面FMC,OM?平面FMC,
∴PG∥平面FMC
点评:本题考查的知识点是直线与平面垂直的性质,直线与平面平行的判定,其中熟练掌握空间直线与平面平行及垂直的判定定理及性质定理,是解答本题的关键.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
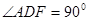 ,G是DF上一动点
,G是DF上一动点 GN垂直AC
GN垂直AC

 在长方形ABEF中,D,C分别是AF和BE的中点,M和N分别是AB和AC的中点,AF=2AB=2a,将平面DCEF沿着DC折起,使角∠ADF=90°,G是DF上一动点,求证:
在长方形ABEF中,D,C分别是AF和BE的中点,M和N分别是AB和AC的中点,AF=2AB=2a,将平面DCEF沿着DC折起,使角∠ADF=90°,G是DF上一动点,求证: