题目内容
“长为L (米)的大型机器零件,在通过传送带的流水线时,为安全起见,零件之间的距离不得小于 kLv2(米).其中v (米/时)是流水线的流速,k为比例系数.现经测定,当流速为60 (米/时) 时,零件之间的安全距离为1.44L.(1)根据给出数据求出比例系数k;
(2)写出流水线上的流量y 关于流水线流速v 的函数关系式; (流量是单位时间内通过的零件数,即
| 速度 | 零件长度+安全距离 |
(3)应该规定多大的流速,才能使同一流水线上的零件流量最大?最大流量是多少?
分析:(1)将流速为60(米/时),安全距离为1.44L代入,可求得k;
(2)由流量是单位时间内通过的零件数,即
可得;
(3)由y=
=
≤
可求.
(2)由流量是单位时间内通过的零件数,即
| 速度 |
| 零件长度+安全距离 |
(3)由y=
| v | ||
L+
|
| 1 | ||||
|
| 1 |
| 25L |
解答:解:(1)由题意d=kLv2,将流速为60(米/时),安全距离为1.44L代入,可求得1.44L=kL×(60)2,
∴k=
;
(2)由流量=
可得y=
;
(3)由题意y=
=
≤
,当且仅当
=
Lv时,即v=50时,流量达到最大为
.
∴k=
| 1 |
| 2500 |
(2)由流量=
| 速度 |
| 零件长度+安全距离 |
| v | ||
L+
|
(3)由题意y=
| v | ||
L+
|
| 1 | ||||
|
| 1 |
| 25L |
| L |
| v |
| 1 |
| 2500 |
| 1 |
| 25L |
点评:本题主要考查函数模型的构建,及利用基本不等式求最值,属于基本题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
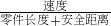 )
) )
)