Question

(2005山东，22)如下图,已知动圆过定点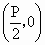，且与直线相切，其中p＞0，

(1)求动圆圆心的轨迹C的方程；

(2)设A、B是轨迹C上异于原点O的两个不同点，直线OA和OB的倾斜角分别为α和β，当α、β变化且α+β为定值θ(0＜θ＜π)时，证明：直线AB恒过定点，并求出该定点的坐标．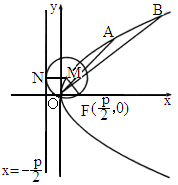

Answer 1

答案：略
解析：

解析：(1)设M为动圆圆心，记为F，过点M作直线的垂线，垂足为N． 由题意知：，即动点M到定点F与定直线的距离相等，由抛物线定义知：点M的轨迹为抛物线，其中为焦点，为准线，所以轨迹方程为． (2)设，由题意得(否则)且． 所以直线AB的斜率存在，设其方程为y=kx＋b． 显然．将y=kx＋b与联立消去x，得． 由韦达定理知 ．　　　　(*) ①当时，即时， ， ， ． 由(*)式知：． 因此直线AB的方程可表示为： ，即k(x＋2p)－y=0． ∴直线AB恒过定点(－2p，0)． ②当，由得 ． 将(*)式代入上式整理化简，得： ． 此时，直线AB的方程可表示为， 即． ∴直线AB恒过定点． ∴由①②知， 当时，直线AB恒过定点(－2p，0)； 当时，直线AB恒过定点．