题目内容
设数列{ }的前n项和为Sn(n∈N?),关于数列{
}的前n项和为Sn(n∈N?),关于数列{ }有下列四个命题:
}有下列四个命题:
(1)若{ }既是等差数列又是等比数列,则an=an+1(n∈N*);
}既是等差数列又是等比数列,则an=an+1(n∈N*);
(2)若Sn=An2+Bn(A,B∈R,A、B为常数),则{ }是等差数列;
}是等差数列;
(3)若Sn=1-(-1)n,则{ }是等比数列;
}是等比数列;
(4)若{ }是等比数列,则Sm,S2m-Sm,S3m-S2m(m∈N*)也成等比数列;其中正确的命题的个数是
}是等比数列,则Sm,S2m-Sm,S3m-S2m(m∈N*)也成等比数列;其中正确的命题的个数是
A.4 B.3 C.2 D.1
【答案】
B
【解析】解:
(1)若{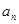 }既是等差数列又是等比数列,则an=an+1(n∈N*);
错误,零常数列不符合
}既是等差数列又是等比数列,则an=an+1(n∈N*);
错误,零常数列不符合
(2)若Sn=An2+Bn(A,B∈R,A、B为常数),则{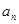 }是等差数列;满足定义
}是等差数列;满足定义
(3)若Sn=1-(-1)n,则{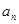 }是等比数列;成立
}是等比数列;成立
(4)若{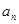 }是等比数列,则Sm,S2m-Sm,S3m-S2m(m∈N*)也成等比数列成立
}是等比数列,则Sm,S2m-Sm,S3m-S2m(m∈N*)也成等比数列成立

练习册系列答案
相关题目