题目内容
已知不等式组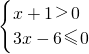 的解集是A,全集U=R
的解集是A,全集U=R
(1)求CUA;
(2)若集合B={y|y=x2-2x,x∈A},C={y|y=1-2x,x∈A},求B∩C,B∪C.
解:(1)∵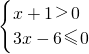 的解集是A={x|-1<x≤2}
的解集是A={x|-1<x≤2}
又∵全集U=R
∴CUA={x|x≤-1或x>2}
(2)∵集合B={y|y=x2-2x,x∈A}
∴B={y|y>0}
∵C={y|y=1-2x,x∈A}
∴C={y|y≥ 或y<-3}
或y<-3}
∴B∩C={y|y≥ }
}
B∪C={y|y>0或y<-3}
分析:(1)首先解二元一次不等式组,确定集合A,然后根据全集U=R,求出CUA.
(2)根据集合B={y|y=x2-2x,x∈A},C={y|y=1-2x,x∈A}分别求出集合B,C.然后求出B∩C,B∪C
点评:本题考查交集并集补集的混合运算,其中涉及到考查二元一次不等式组的问题.属于基础题
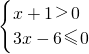 的解集是A={x|-1<x≤2}
的解集是A={x|-1<x≤2}又∵全集U=R
∴CUA={x|x≤-1或x>2}
(2)∵集合B={y|y=x2-2x,x∈A}
∴B={y|y>0}
∵C={y|y=1-2x,x∈A}
∴C={y|y≥
 或y<-3}
或y<-3}∴B∩C={y|y≥
 }
}B∪C={y|y>0或y<-3}
分析:(1)首先解二元一次不等式组,确定集合A,然后根据全集U=R,求出CUA.
(2)根据集合B={y|y=x2-2x,x∈A},C={y|y=1-2x,x∈A}分别求出集合B,C.然后求出B∩C,B∪C
点评:本题考查交集并集补集的混合运算,其中涉及到考查二元一次不等式组的问题.属于基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的解集是不等式
的解集是不等式 的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是_______________.
的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是_______________. 的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是____________________________________.
的解集是不等式2x2-9x+a<0的解集的子集,则实数a的取值范围是____________________________________. 的解集是不等式
的解集是不等式 的解集是不等式
的解集是不等式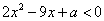 的解集的子集,
的解集的子集,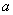 的取值范围是
.
的取值范围是
.