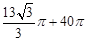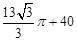题目内容
四棱锥
的顶点P在底面ABCD中的投影恰好是A，其三视图如图所示，则四棱锥的表面积为
A． a2 | B．2a2 | C． a2 | D．(2+)a2 |
D
解析考点：由三视图求面积、体积．
专题：计算题．
分析：由四棱锥P-ABCD的顶点P在底面ABCD中的投影恰好是A，我们易得PA是棱锥的高，由三视图我们易得底面边长，及棱锥的高均为a，由此我们易求出各棱的长，进而求出各个面的面积，进而求出四棱锥P-ABCD的表面积．
解答：解：由三视图我们易得四棱锥P-ABCD的底面棱长为a，高PA=a
则四棱锥P-ABCD的底面积为：a2
侧面积为：S△PAB+S△PBC+S△PCD+S△PAD=2×
×a2+=2××a×
a=2a2+a2，
则四棱锥P-ABCD的表面积为 2a2+a2
故选D．
点评：本题考查由三视图求几何体的表面积，考查由三视图看出几何体中各个部分的长度，本题是一个基础题．
练习册系列答案
相关题目
如图是由一些相同的小正方体构成的主体图形的三种视图，构成这个立体图形的小正方体的个数是
| A．3 | B．4 | C．5 | D．6 |
、一个圆柱的侧面展开图是一个正方形，这个圆柱的全面积与侧面积的比是（ ）.
A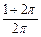． | B． | C． | D． |
+
若圆柱、圆锥的底面直径和高都等于球的直径，则圆柱、圆锥、球的体积的比为（ ）
| A．1:2:3 | B．2：3：4 | C．3:2:4 | D．3:1:2 |
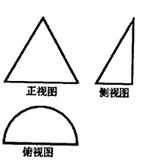
的菱形，则该棱柱的体积等于 （ ）
