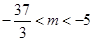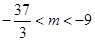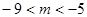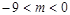题目内容
已知函数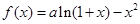 ,当
,当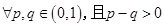 时,不等式
时,不等式
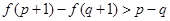 恒成立,则实数
恒成立,则实数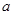 的取值范围为( )
的取值范围为( )
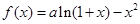 ,当
,当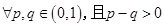 时,不等式
时,不等式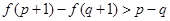 恒成立,则实数
恒成立,则实数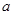 的取值范围为( )
的取值范围为( )A. | B. | C. | D. |
B
试题分析:由已知得,
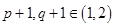 ,
,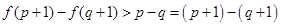 ,因为
,因为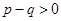 ,所以
,所以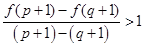 ,所以函数图像上在
,所以函数图像上在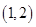 区间内的任意两点连线的斜率大于1.函数
区间内的任意两点连线的斜率大于1.函数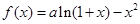 的导函数为
的导函数为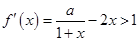 在区间
在区间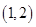 上恒成立,即
上恒成立,即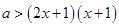 在区间
在区间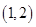 上恒成立,设函数
上恒成立,设函数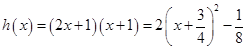 ,它在区间
,它在区间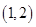 上是单调递增的,所以其最大值为
上是单调递增的,所以其最大值为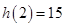 ,所以实数
,所以实数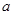 的取值范围为
的取值范围为 .
.
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
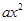 -(a+2)x+lnx.
-(a+2)x+lnx.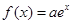 ,
,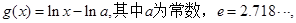 且
且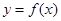
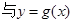 的图象在它们与坐标轴交点处的切线互相平行.
的图象在它们与坐标轴交点处的切线互相平行.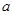 的值;
的值;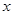 使不等式
使不等式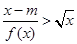 成立,求实数
成立,求实数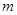 的取值范围;
的取值范围;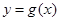 公共定义域内的任意实数
公共定义域内的任意实数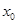 ,我们把
,我们把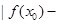
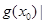 的值称为两函数在
的值称为两函数在 .
. 时,求函数
时,求函数 的最大值;
的最大值; 其图象上任意一点
其图象上任意一点 处切线的斜率
处切线的斜率 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; ,
, ,方程
,方程 有唯一实数解,求正数
有唯一实数解,求正数 的值.
的值. (
(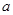 ≠0,
≠0, ,求函数
,求函数 的极值和单调区间;
的极值和单调区间; ,使得
,使得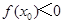 成立,求实数
成立,求实数 .
. 是函数
是函数 的极值点,求
的极值点,求 的值;
的值; 的单调区间.
的单调区间.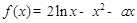 .
.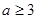 时,讨论函数
时,讨论函数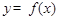 在[
在[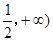 上的单调性;
上的单调性;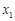 ,
,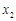
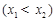 是函数
是函数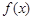 的两个零点,
的两个零点,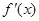 为函数
为函数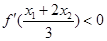 .
. 的图象在
的图象在 处的切线与圆
处的切线与圆 相切,则
相切,则 的最大值是( )
的最大值是( )

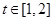 ,函数
,函数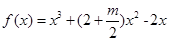 在区间
在区间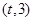 上总不是单调函数,求
上总不是单调函数,求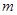 的取值范围是( )
的取值范围是( )