题目内容
(本小题14分)已知函数f(x)＝3x，且f(a＋2)＝18，g(x)＝3ax－4x的定义域为区间[－1,1]．(1)求g(x)的解析式；(2)判断g(x)的单调性．
解：(1)∵f(a＋2)＝18，f(x)＝3x.
∴3a＋2＝18，即3a＝2.
故g(x)＝(3a)x－4x＝2x－4x，x∈[－1,1]．
(2)g(x)＝－(2x)2＋2x＝－2＋.
当x∈[－1,1]时，2x∈.令t＝2x，
由二次函数单调性得
－2＋在上是减函数，
∴函数g(x)在[－1,1]上是减函数
∴3a＋2＝18，即3a＝2.
故g(x)＝(3a)x－4x＝2x－4x，x∈[－1,1]．
(2)g(x)＝－(2x)2＋2x＝－2＋.
当x∈[－1,1]时，2x∈.令t＝2x，
由二次函数单调性得
－2＋在上是减函数，
∴函数g(x)在[－1,1]上是减函数
略
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
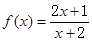，试证明f(x)在区间(-2,+∞)上是增函数，并求出该函数在区间[1,4]上的最大值和最小值.
的值域是
.
.
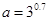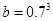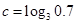的大小顺序为( )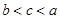
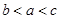
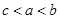
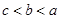
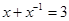，则
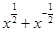值为（ ）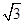
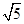
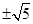
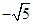
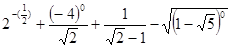,结果是（ ）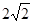
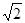
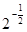
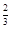＋lg4＋2lg5＝__________
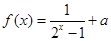是奇函数，则
．
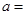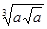的结果是（ ）
