题目内容
已知向量 、
、 满足|
满足| |=|
|=| |=1,且
|=1,且 与
与 的夹角为60°.
的夹角为60°.
(1)求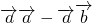 ;
;
(2)若 与
与 +λ
+λ 垂直,求实数λ的值.
垂直,求实数λ的值.
解:(1)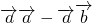 =|
=| |2-|
|2-| ||
|| |cos60°=
|cos60°=
(2)∵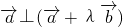
∴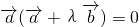
即
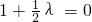
解得λ=-2
分析:(1)利用向量模的性质:向量的平方等于向量模的平方及向量的数量积公式求出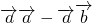 的值.
的值.
(2)利用向量垂直的充要条件: ?
? 列出方程,利用向量的数量积公式及向量模的性质求出实数λ的值.
列出方程,利用向量的数量积公式及向量模的性质求出实数λ的值.
点评:解决向量垂直问题一个利用向量垂直的充要条件:它们的数量积为0;解决向量的模的问题常利用模的性质:向量模的平方等于向量的平方.
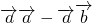 =|
=| |2-|
|2-| ||
|| |cos60°=
|cos60°=
(2)∵
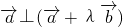
∴
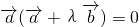
即

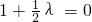
解得λ=-2
分析:(1)利用向量模的性质:向量的平方等于向量模的平方及向量的数量积公式求出
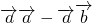 的值.
的值.(2)利用向量垂直的充要条件:
 ?
? 列出方程,利用向量的数量积公式及向量模的性质求出实数λ的值.
列出方程,利用向量的数量积公式及向量模的性质求出实数λ的值.点评:解决向量垂直问题一个利用向量垂直的充要条件:它们的数量积为0;解决向量的模的问题常利用模的性质:向量模的平方等于向量的平方.

练习册系列答案
相关题目
 、
、 满足
满足 ,则
,则 .
. ,实数
,实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.1 C.
B.1 C. D.
D.
 ,
, 满足
满足 ,
, ,
, ,则
,则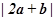 的值为_______.
的值为_______.