题目内容
已知高为9的三棱锥P-ABC中，三个侧面与底面ABC所成的二面角都是60°，求这个三棱锥的内切球O的体积．分析：由题意推知三棱锥是正三棱锥，利用三棱锥的高，求出斜高，然后求出三棱锥的内切球O的半径，即可求出球的体积．
解答：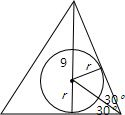
解：高为9的三棱锥P-ABC中，三个侧面与底面ABC所成的二面角都是60°，
说明三棱锥是正三棱锥，顶点在底面的射影是正三角形的中心，
三棱锥的斜高为：
=6
内切球的半径为：
=
，r=3
这个三棱锥的内切球O的体积：
r3=36π．
解：高为9的三棱锥P-ABC中，三个侧面与底面ABC所成的二面角都是60°，说明三棱锥是正三棱锥，顶点在底面的射影是正三角形的中心，
三棱锥的斜高为：
| 9 | ||||
|
| 3 |
内切球的半径为：
| r | ||
3
|
| ||
| 3 |
这个三棱锥的内切球O的体积：
| 4π |
| 3 |
点评：本题考查球的体积，空间想象能力，计算能力，能够正确处理几何体与球的图形关系是解题关键，最好是画出图形，帮助理解，本题是基础题．
练习册系列答案
阅读快车系列答案
相关题目