题目内容
设an=n+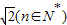 ,求证:数列{an}中任意不同的三项都不可能成为等比数列.
,求证:数列{an}中任意不同的三项都不可能成为等比数列.
【答案】分析:假设数列{an}中存在三项ap,aq,ar(p,q,r互不相等)成等比数列,则根据等比中项的性质可知aq2=apar.把ap,aq,ar代入求得(q2-pr)+(2q-p-r) =0进而推断出
=0进而推断出 ,求得p=r,与p≠r矛盾.进而可知假设不成立.
,求得p=r,与p≠r矛盾.进而可知假设不成立.
解答:证明:假设数列{an}中存在三项ap,aq,ar(p,q,r互不相等)成等比数列,则aq2=apar.
即(q+ )2=(p+
)2=(p+ )(r+
)(r+ ).
).
∴(q2-pr)+(2q-p-r) =0
=0
∵p,q,r∈N*,
∴ ,
,
∴( )2=pr,(p-r)2=0,
)2=pr,(p-r)2=0,
∴p=r.
与p≠r矛盾.
所以数列{an}中任意不同的三项都不可能成等比数列.
点评:本小题考查数列的基本知识,考查等差数列的概念、通项公式与前n项和公式,考查等比数列的概念与性质,考查化归的数学思想方法以及推理和运算能力.
 =0进而推断出
=0进而推断出 ,求得p=r,与p≠r矛盾.进而可知假设不成立.
,求得p=r,与p≠r矛盾.进而可知假设不成立.解答:证明:假设数列{an}中存在三项ap,aq,ar(p,q,r互不相等)成等比数列,则aq2=apar.
即(q+
 )2=(p+
)2=(p+ )(r+
)(r+ ).
).∴(q2-pr)+(2q-p-r)
 =0
=0∵p,q,r∈N*,
∴
 ,
,∴(
 )2=pr,(p-r)2=0,
)2=pr,(p-r)2=0,∴p=r.
与p≠r矛盾.
所以数列{an}中任意不同的三项都不可能成等比数列.
点评:本小题考查数列的基本知识,考查等差数列的概念、通项公式与前n项和公式,考查等比数列的概念与性质,考查化归的数学思想方法以及推理和运算能力.

练习册系列答案
相关题目