题目内容
椭圆25x2-150x+9y2+18y+9=0的两个焦点坐标是
- A.(-3,5),(-3,-3)
- B.(3,3),(3,-5)
- C.(1,1),(-7,1)
- D.(7,-1),(-1,-1)
B
分析:把椭圆的方程化为标准方程后,找出a与b,根据a2=b2+c2求出c的值,然后根据椭圆的中心坐标即可得到两焦点的坐标.
解答:把椭圆方程25x2-150x+9y2+18y+9=0化为标准方程为: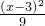 +
+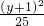 =1,
=1,
所以a=5,b=3,则c= =4,且椭圆的中心为(3,-1),
=4,且椭圆的中心为(3,-1),
则两焦点坐标分别为(3,3)和(3,-5).
故选B
点评:此题考查学生灵活运用椭圆的简单性质化简求值,是一道中档题.
分析:把椭圆的方程化为标准方程后,找出a与b,根据a2=b2+c2求出c的值,然后根据椭圆的中心坐标即可得到两焦点的坐标.
解答:把椭圆方程25x2-150x+9y2+18y+9=0化为标准方程为:
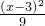 +
+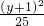 =1,
=1,所以a=5,b=3,则c=
 =4,且椭圆的中心为(3,-1),
=4,且椭圆的中心为(3,-1),则两焦点坐标分别为(3,3)和(3,-5).
故选B
点评:此题考查学生灵活运用椭圆的简单性质化简求值,是一道中档题.

练习册系列答案
相关题目
椭圆25x2-150x+9y2+18y+9=0的两个焦点坐标是( )
| A、(-3,5),(-3,-3) | B、(3,3),(3,-5) | C、(1,1),(-7,1) | D、(7,-1),(-1,-1) |