题目内容
 中国跳水运动员进行10 m跳台跳水训练时,身体(看成一点)在空中的运动路线为如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面10
中国跳水运动员进行10 m跳台跳水训练时,身体(看成一点)在空中的运动路线为如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面10| 2 |
| 3 |
(1)求这条抛物线的解析式.
(2)在某次试跳中,测得运动员在空中的运动路线是(1)中的抛物线,且运动员在空中调整好入水姿势时,距池边的水平距离为3
| 3 |
| 5 |
(3)要使此次跳水不至于失误,该运动员按(1)中抛物线运行,且运动员在空中调整好入水姿势时,距池边的水平距离至多应为多少?
分析:(1)根据题意先设出抛物线的方程,根据题意可知O,B的坐标和A的纵坐标,把(0,0)点代入抛物线方程求得c,点A的纵坐标求得a,b和c的关系把(2,-10)代入抛物线方程求得a,b令一关系式,联立求得a和b,则抛物线方程可得.
(2)把x═3
-2代入抛物线方程求得y,进而求得运动员距水面的高度,与5进行比较判断出答案.
(3)当运动员在x轴上方,即y>0的区域内完成动作并做好入水姿势时,运动员很难做到.故可看当y<0时,要使跳水不出现失误y的范围,进而利用二次函数的单调性求得x的范围.
(2)把x═3
| 3 |
| 5 |
(3)当运动员在x轴上方,即y>0的区域内完成动作并做好入水姿势时,运动员很难做到.故可看当y<0时,要使跳水不出现失误y的范围,进而利用二次函数的单调性求得x的范围.
解答:解:(1)在给定的直角坐标系下,设最高点为A,入水点为B,抛物线的解析式为
y=ax2+bx+c.
由题意知,O、B两点的坐标依次为(0,0)、(2,-10),且顶点A的纵坐标为
,c=0,
所以有
=
,
4a+2b+c=-10.a=-
,
解之得b=
,c=0
或a=-
,b=-2,c=0.
∵抛物线对称轴在y轴右侧,∴-
>0.
又∵抛物线开口向下,∴a<0.
∴b>0,后一组解舍去.
∴a=-
,b=
,c=0.
∴抛物线的解析式为y=-
x2+
x.
(2)当运动员在空中距池边的水平距离为3
m时,即x=3
-2=
时,
y=(-
)×(
)2+
×
=-
,
∴此时运动员距水面的高为
10-
=
<5.
因此,此次跳水会出现失误.
(3)当运动员在x轴上方,即y>0的区域内完成动作并做好入水姿势时,当然不会失误,但很难做到.
∴当y<0时,要使跳水不出现失误,
则应有|y|≤10-5,即-y≤5.
∴有
x2-
x≤5,
解得2-
≤x≤2+
.
∴运动员此时距池边的距离至多为2+2+
=4+
m.
y=ax2+bx+c.
由题意知,O、B两点的坐标依次为(0,0)、(2,-10),且顶点A的纵坐标为
| 2 |
| 3 |
所以有
| 4ac-b2 |
| 4a |
| 2 |
| 3 |
4a+2b+c=-10.a=-
| 25 |
| 6 |
解之得b=
| 10 |
| 3 |
或a=-
| 3 |
| 2 |
∵抛物线对称轴在y轴右侧,∴-
| b |
| 2a |
又∵抛物线开口向下,∴a<0.
∴b>0,后一组解舍去.
∴a=-
| 25 |
| 6 |
| 10 |
| 3 |
∴抛物线的解析式为y=-
| 25 |
| 6 |
| 10 |
| 3 |
(2)当运动员在空中距池边的水平距离为3
| 3 |
| 5 |
| 3 |
| 5 |
| 8 |
| 5 |
y=(-
| 25 |
| 6 |
| 8 |
| 5 |
| 10 |
| 3 |
| 8 |
| 5 |
| 16 |
| 3 |
∴此时运动员距水面的高为
10-
| 16 |
| 3 |
| 14 |
| 3 |
因此,此次跳水会出现失误.
(3)当运动员在x轴上方,即y>0的区域内完成动作并做好入水姿势时,当然不会失误,但很难做到.
∴当y<0时,要使跳水不出现失误,
则应有|y|≤10-5,即-y≤5.
∴有
| 25 |
| 6 |
| 10 |
| 3 |
解得2-
| 34 |
| 34 |
∴运动员此时距池边的距离至多为2+2+
| 34 |
| 34 |
点评:本题主要考查了抛物线的应用,二次函数的性质,以及待定系数法求函数解析式问题.解题的关键是建立数学模型,把实际问题与数学问题相联系.

练习册系列答案
相关题目
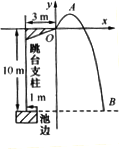
 m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误. m,问此次跳水会不会失误?并通过计算说明理由.
m,问此次跳水会不会失误?并通过计算说明理由.
 m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误. m,问此次跳水会不会失误?并通过计算说明理由.
m,问此次跳水会不会失误?并通过计算说明理由.
 m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
m,入水处距池边的距离为4 m,同时,运动员在距水面高度为5 m或5 m以上时,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误. m,问此次跳水会不会失误?并通过计算说明理由.
m,问此次跳水会不会失误?并通过计算说明理由.