题目内容
两个腰长均为1的等腰直角△ABC1和△ABC2所在的平面构成60°的二面角,则点C1和C2之间的距离等于分析:有三种情况:
①若AB是斜边,则根据题中二面角的大小,要把这个条件用起来的话,首先要作出此二面角的平面角,可以取AB中点M,连接MC1、MC2,则∠C1MC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,进而可以求得答案;
②若AB是直角边,则∠C1AC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,进一步可得答案.
③如图3所示:AB为公共直角边时,C1在靠近A的这侧,但是C2在靠近B的那侧.
①若AB是斜边,则根据题中二面角的大小,要把这个条件用起来的话,首先要作出此二面角的平面角,可以取AB中点M,连接MC1、MC2,则∠C1MC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,进而可以求得答案;
②若AB是直角边,则∠C1AC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,进一步可得答案.
③如图3所示:AB为公共直角边时,C1在靠近A的这侧,但是C2在靠近B的那侧.
解答: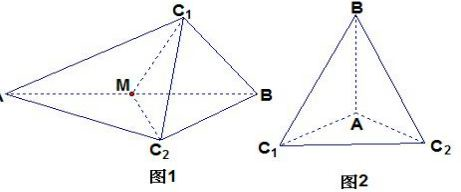 解:如图所示,有两种情况:
解:如图所示,有两种情况:
①如图1所示:当AB为斜边时,取AB中点M,连接MC1、MC2,
∵△ABC1和△ABC2均为等腰直角三角形,
∴MC1⊥AB,MC2⊥AB,则∠C1MC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,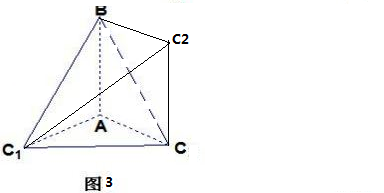
∴∠C1MC2=60°
又∵MC1=MC2=
∴C1C2=
②如图2所示:当AB为直角边时,
∵BA⊥AC1,BA⊥AC2,
∴∠C1AC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,
∴∠C1AC2=60°
又∵C1A=C2A=1
∴C1C2=1
③如图3所示:AB为公共直角边时,C1在靠近A的这侧,但是C2在靠近B的那侧,
此时C1C2=
综上所述:点C1和C2之间的距离等于
或1
.
故答案为:
或1或
.
 解:如图所示,有两种情况:
解:如图所示,有两种情况:①如图1所示:当AB为斜边时,取AB中点M,连接MC1、MC2,
∵△ABC1和△ABC2均为等腰直角三角形,
∴MC1⊥AB,MC2⊥AB,则∠C1MC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,

∴∠C1MC2=60°
又∵MC1=MC2=
| ||
| 2 |
∴C1C2=
| ||
| 2 |
②如图2所示:当AB为直角边时,
∵BA⊥AC1,BA⊥AC2,
∴∠C1AC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,
∴∠C1AC2=60°
又∵C1A=C2A=1
∴C1C2=1
③如图3所示:AB为公共直角边时,C1在靠近A的这侧,但是C2在靠近B的那侧,
此时C1C2=
| 2 |
综上所述:点C1和C2之间的距离等于
| ||
| 2 |
| 2 |
故答案为:
| ||
| 2 |
| 2 |
点评:本小题主要考查点、线、面之间的距离计算,二面角及其度量等基本知识,同时考查空间想象能力和推理、运算能力.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目