题目内容
已知x+y-3=0,则
的最小值等于
.
| (x-2)2+(y+1)2 |
| 2 |
| 2 |
分析:法一:由题意可得y=-x+3则
=
=
=
,由二次函数的性质可求
法二:由题意可得
是点(2,-1)到直线x+y-3=0上的任意一点(x,y)的距离,所求的最小值即为点(2,-1)到直线x+y-3=0的距离,由点到直线的距离公式可求
| (x-2)2+(y+1)2 |
| x2-4x+4+x2-8x+16 |
=
| 2x2-12x+20 |
| 2(x-3)2+2 |
法二:由题意可得
| (x-2)2+(y+1)2 |
解答:解:法一:由题意可得y=-x+3
则
=
=
=
由二次函数的性质可知,当x=3时,所求式子的值最小
故答案为
法二:由题意可得
即是点(2,-1)到直线x+y-3=0上的任意一点(x,y)的距离
所求的最小值即为点(2,-1)到直线x+y-3=0的距离d=
=
故答案为
则
| (x-2)2+(y+1)2 |
| x2-4x+4+x2-8x+16 |
=
| 2x2-12x+20 |
| 2(x-3)2+2 |
由二次函数的性质可知,当x=3时,所求式子的值最小
| 2 |
故答案为
| 2 |
法二:由题意可得
| (x-2)2+(y+1)2 |
所求的最小值即为点(2,-1)到直线x+y-3=0的距离d=
| |2-1-3| | ||
|
| 2 |
故答案为
| 2 |
点评:本题主要考查了点到直线的距离公式的应用,解题的关键是把所求的式子转化为距离问题,还要注意函数思想在解题中的应用.

练习册系列答案
相关题目
 的最小值.
的最小值.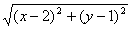 的最小值.
的最小值. 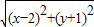 的最小值等于 .
的最小值等于 . 的最小值等于 .
的最小值等于 .