题目内容
 如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B(其中
如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+B(其中| π | 2 |
分析:(1)由图象的最高点与最低点易于求出这段时间的最大温差;
(2)A、b可由图象直接得出,ω由周期求得,然后通过特殊点求φ,则问题解决.
(2)A、b可由图象直接得出,ω由周期求得,然后通过特殊点求φ,则问题解决.
解答:解:(1)由图示,这段时间的最大温差是30-10=20℃,
(2)图中从6时到14时的图象是函数y=Asin(ωx+∅)+b的半个周期,
∴
•
=14-6,解得ω=
,
由图示,A=
(30-10)=10,B=
(10+30)=20,
这时,y=10sin(
x+φ)+20,
将x=6,y=10代入上式,可取 φ=
π,
综上,所求的解析式为 y=10sin(
x+
)+20,x∈[6,14].
故答案为:20;y=10sin(
x+
)+20,x∈[6,14]
(2)图中从6时到14时的图象是函数y=Asin(ωx+∅)+b的半个周期,
∴
| 1 |
| 2 |
| 2π |
| ω |
| π |
| 8 |
由图示,A=
| 1 |
| 2 |
| 1 |
| 2 |
这时,y=10sin(
| π |
| 8 |
将x=6,y=10代入上式,可取 φ=
| 3 |
| 4 |
综上,所求的解析式为 y=10sin(
| π |
| 8 |
| 3π |
| 4 |
故答案为:20;y=10sin(
| π |
| 8 |
| 3π |
| 4 |
点评:本题主要考查由函数y=Asin(ωx+∅)+b的部分图象确定其解析式的基本方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中
如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中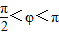 ),那么这一天6时至14时温差的最大值是 °C;与图中曲线对应的函数解析式是 .
),那么这一天6时至14时温差的最大值是 °C;与图中曲线对应的函数解析式是 .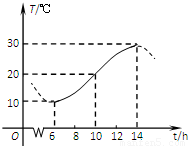
 ),那么与图中曲线对应的函数解析式是 .
),那么与图中曲线对应的函数解析式是 .
 (其中
(其中 ),
那么这一天6时至14时温差的最大值是________
),
那么这一天6时至14时温差的最大值是________ ;与图中曲线对应的函数解析式是______________
;与图中曲线对应的函数解析式是______________