题目内容
设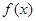 是定义在
是定义在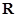 上的偶函数,对任意的
上的偶函数,对任意的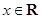 ,都有
,都有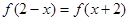 ,且当
,且当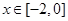 时,
时,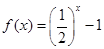 ,若关于
,若关于 的方程
的方程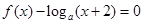
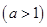 在区间
在区间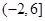 内恰有三个不同实根,则实数
内恰有三个不同实根,则实数 的取值范围是 .
的取值范围是 .
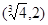
解析试题分析:∵对于任意的x∈R,都有f(2-x)=f(x+2),∴函数f(x)的图象关于直线x=2对称,又∵当x∈[-2,0]时,f(x)=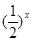 -1,且函数f(x)是定义在R上的偶函数,若在区间(-2,6)内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,则函数y=f(x)与y=loga(x+2)在区间(-2,6)上有三个不同的交点,如下图所示:
-1,且函数f(x)是定义在R上的偶函数,若在区间(-2,6)内关于x的方程f(x)-loga(x+2)=0恰有3个不同的实数解,则函数y=f(x)与y=loga(x+2)在区间(-2,6)上有三个不同的交点,如下图所示: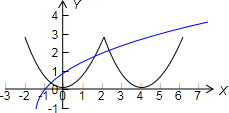
又f(-2)=f(2)=3,则有 loga(2+2)<3,且loga(6+2)≥3,解得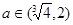 .
.
考点:1.指数函数与对数函数的图象与性质;2.函数的零点与方程根的关系

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
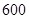 吨,每次都购买
吨,每次都购买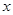 吨,运费为
吨,运费为 万元/次,一年的总存储费用为
万元/次,一年的总存储费用为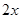 万元,若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.
万元,若要使一年的总运费与总存储费用之和最小,则每次需购买 吨.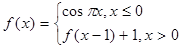 ,则
,则 的值为 .
的值为 .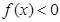 的解集为{
的解集为{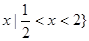 ,则
,则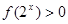 的解集为 .
的解集为 . 的图象如图,则满足
的图象如图,则满足 的
的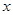 的取值范 .
的取值范 .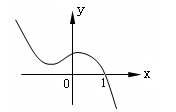
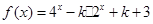 有唯一零点,则实数
有唯一零点,则实数 的取值范围是______.
的取值范围是______.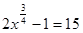 的解为
的解为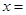
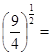 .
.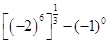 的值为 .
的值为 .