题目内容
登山运动员10人,平均分为两组,其中熟悉道路的4人,每组都需要2人,那么不同的分配方法种数是
- A.30
- B.60
- C.120
- D.240
B
分析:本题可以采用分步计数原理来解,先将4个熟悉道路的人平均分成两组,再将余下的6人平均分成两组,前两个分组都是平均分组,然后这四个组自由搭配还有A22种,根据分步计数原理得到结果.
解答:本题可以采用分步计数原理来解,
先将4个熟悉道路的人平均分成两组有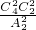 .
.
再将余下的6人平均分成两组有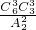 .
.
然后这四个组自由搭配还有A22种,
故最终分配方法有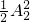 ×
× C42•C63=60(种)
C42•C63=60(种)
故选B
点评:本题考查的是排列组合问题,把排列问题包含在实际问题中,解题的关键是看清题目的实质,把实际问题转化为数学问题,解出结果以后再还原为实际问题.
分析:本题可以采用分步计数原理来解,先将4个熟悉道路的人平均分成两组,再将余下的6人平均分成两组,前两个分组都是平均分组,然后这四个组自由搭配还有A22种,根据分步计数原理得到结果.
解答:本题可以采用分步计数原理来解,
先将4个熟悉道路的人平均分成两组有
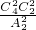 .
.再将余下的6人平均分成两组有
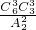 .
.然后这四个组自由搭配还有A22种,
故最终分配方法有
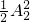 ×
× C42•C63=60(种)
C42•C63=60(种)故选B
点评:本题考查的是排列组合问题,把排列问题包含在实际问题中,解题的关键是看清题目的实质,把实际问题转化为数学问题,解出结果以后再还原为实际问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
登山运动员10人,平均分为两组,其中熟悉道路的4人,每组都需要2人,那么不同的分配方法种数是( )
| A、30 | B、60 | C、120 | D、240 |