题目内容
设函数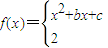 其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个不相同的实数根,求a取值的集合.
【答案】分析:(1)注意关键字:当且仅当x=-2时,函数f(x)取得最小值-2,说明表达式中的二次函数图象关于直线x=-2对称,并且f(-2)=-2,由此可得出b、c的值,从而得到函数f(x)的表达式;
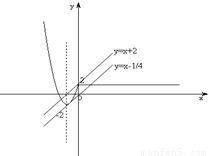
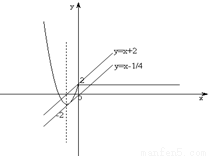
(2)作出函数y=f(x)的图象,再作出直线l:y=x+a,通过先求出两图象恰有两个不同公共点的临界位置,再平移直线,根据直线在y轴上截距的取值范围,最后求得a取值的集合.
解答:解:(1)∵当且仅当x=-2时,函数f(x)取得最小值-2
∴二次函数y=x2+bx+c图象关于直线x=-2对称且f(-2)=-2
可得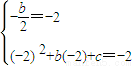 ⇒
⇒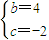
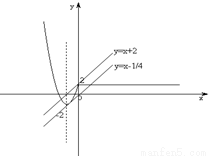
∴函数f(x)的表达式为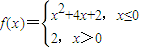
(2)同一坐标系里,作出函数y=f(x)的图象和直线l:y=x+a,可得:
①当a=2时,直线l与y=f(x)的图象有两个不同的公共点,
②将直线向下平移至两图象相切,此时由x2+4x+2=x+a得
x2+3x+2-a=0,根的判别式△=9-4(2-a)=0,⇒a=-
综合①②这两种特殊位置,可得当- ≤a≤2时,直线l在图中两条件平行线之间运动(含边界)
≤a≤2时,直线l在图中两条件平行线之间运动(含边界)
此时两图象有两个或三个公共点,相应地方程有至少两个不相同的实数根
所以a取值的集合是: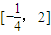
点评:本题着重考查了函数解析式求解的常用方法和根的存在性及根的个数判断等知识点,属于中档题.采用数形结合与分类讨论,使本题化难为易,迎刃而解.
(2)作出函数y=f(x)的图象,再作出直线l:y=x+a,通过先求出两图象恰有两个不同公共点的临界位置,再平移直线,根据直线在y轴上截距的取值范围,最后求得a取值的集合.
解答:解:(1)∵当且仅当x=-2时,函数f(x)取得最小值-2
∴二次函数y=x2+bx+c图象关于直线x=-2对称且f(-2)=-2
可得
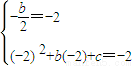 ⇒
⇒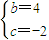

∴函数f(x)的表达式为
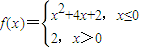
(2)同一坐标系里,作出函数y=f(x)的图象和直线l:y=x+a,可得:
①当a=2时,直线l与y=f(x)的图象有两个不同的公共点,
②将直线向下平移至两图象相切,此时由x2+4x+2=x+a得
x2+3x+2-a=0,根的判别式△=9-4(2-a)=0,⇒a=-

综合①②这两种特殊位置,可得当-
 ≤a≤2时,直线l在图中两条件平行线之间运动(含边界)
≤a≤2时,直线l在图中两条件平行线之间运动(含边界)此时两图象有两个或三个公共点,相应地方程有至少两个不相同的实数根
所以a取值的集合是:
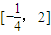
点评:本题着重考查了函数解析式求解的常用方法和根的存在性及根的个数判断等知识点,属于中档题.采用数形结合与分类讨论,使本题化难为易,迎刃而解.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 (2009•成都模拟)设函数
(2009•成都模拟)设函数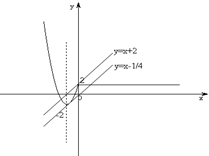 设函数
设函数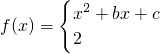 其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.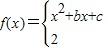 其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.