题目内容
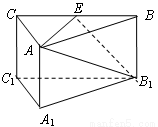
如图,三棱柱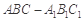 中,侧棱与底面垂直,
中,侧棱与底面垂直,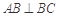 ,
,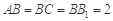 ,
,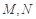 分别是
分别是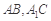 的中点
的中点
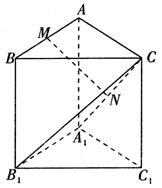
(1)求证: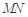 ∥平面
∥平面 ;
;
(2)求证: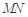 ⊥平面
⊥平面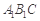 ;
;
(3)求三棱锥的体积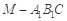 的体积.
的体积.
【答案】
(1)证明过程详见解析;(2)证明过程详见解析;(3)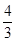 .
.
【解析】
试题分析:本题主要以三棱柱为几何背景考查线面平行、线面垂直和几何体体积等基础知识,考查空间想象能力、运算能力和推理论证能力.第一问,先根据题意作出辅助线,在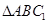 中,利用中位线的性质得
中,利用中位线的性质得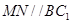 ,再由线面平行的判定,得证;第二问,由已知条件可以判断四边形
,再由线面平行的判定,得证;第二问,由已知条件可以判断四边形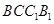 是正方形,所以对角线互相垂直,所以
是正方形,所以对角线互相垂直,所以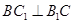 ,又由于第一问得
,又由于第一问得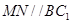 ,所以
,所以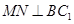 ,再由已知证
,再由已知证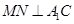 即可,由已知边长,得
即可,由已知边长,得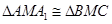 ,所以
,所以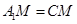 ,所以
,所以 为等腰三角形,而
为等腰三角形,而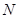 为中点,所以
为中点,所以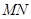 为高,得证,再利用线面垂直的判定即可得证;第三问,利用等体积法将三棱锥进行转化,找到已知条件求体积.
为高,得证,再利用线面垂直的判定即可得证;第三问,利用等体积法将三棱锥进行转化,找到已知条件求体积.
试题解析:(1)证明:连结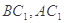 ,显然
,显然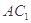 过点
过点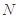
∵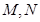 分别是
分别是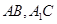 的中点, ∴
的中点, ∴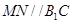 ,
,
又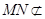 平面
平面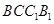 ,
,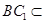 平面
平面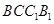 ,∴
,∴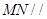 平面
平面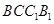 ,
,
(2)∵三棱柱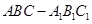 中,侧棱与底面垂直,
中,侧棱与底面垂直,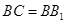 ,
,
∴四边形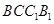 是正方形,∴
是正方形,∴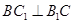 ,
,
由(1)知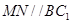 ,∴
,∴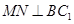 ,
,
连结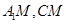 ,由
,由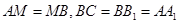 ,知
,知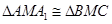 ,
,
∴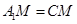 ,又易知
,又易知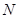 是
是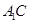 的中点,∴
的中点,∴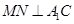 ,
,
∴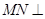 平面
平面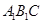 .
.
(3)因为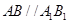 ,所以三棱锥
,所以三棱锥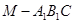 与三棱锥
与三棱锥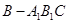 的体积相等,
的体积相等,
故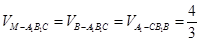 .
.
考点:1.中位线的性质;2.线面平行的判定;3.三角形全等;4.线面垂直的判定;5.等体积法.

练习册系列答案
相关题目
 中,侧棱
中,侧棱 底面
底面 ,
,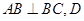 为
为 的中点,
的中点, 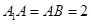 ,
,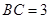 .
.
 平面
平面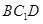 ;
;  的体积.
的体积.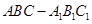 中,侧棱
中,侧棱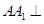 底面
底面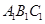 ,底面三角形
,底面三角形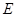 是
是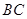 中点,则下列叙述正确的是:
中点,则下列叙述正确的是: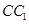 与
与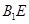 是异面直线
B.
是异面直线
B.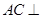 平面
平面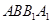
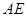 ,
,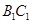 为异面直线,且
为异面直线,且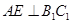 D.
D.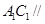 平面
平面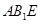
 中,侧棱
中,侧棱 底面
底面 ,底面三角形
,底面三角形 是
是 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )

 与
与 是异面直线
是异面直线 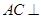 平面
平面
 平面
平面
 ,
, 为异面直线,且
为异面直线,且
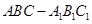 中,侧棱
中,侧棱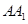 垂直底面
垂直底面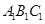 ,底面三角形
,底面三角形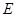 是
是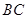 中点,则下列叙述正确的是( )
中点,则下列叙述正确的是( )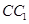 与
与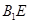 是异面直线
B.
是异面直线
B.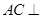 平面
平面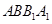
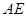 ,
,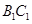 为异面直线,且
为异面直线,且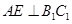 D.
D.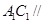 平面
平面