题目内容
在平行四边形OABC中,已知过点C的直线与线段OA,OB分别相交于点M,N.若| OM |
| OA |
| ON |
| OB |
(1)求证:x与y的关系为y=
| x |
| x+1 |
(2)设f(x)=
| x |
| x+1 |
(3)在(2)的条件下,不等式F(x)<-x+a在x∈[2k,2k+1](k∈N)上恒成立,求实数a的取值范围.
分析:(1)利用平行四边形对边平行且相等以及平行线分线段成比例可得x与y的关系.
(2)F(x)图象关于直线x=1对称?F(2-x)=F(x)?F(x+2)=F(-x)再利用F(x)=F(-x)可得F(x+2)=F(x).
在把x∈[2k,2k+1]转化为x-2k∈[0,1],利用x∈[0,1]时F(x)=f(x)可得x∈[2k,2k+1](k∈N)时的解析式.
(3)利用转化的思想把F(x)<-x+a转化为a>1+x-
对x∈[2k,2k+1](k∈N)恒成立,再求后面的最大值即可.
(2)F(x)图象关于直线x=1对称?F(2-x)=F(x)?F(x+2)=F(-x)再利用F(x)=F(-x)可得F(x+2)=F(x).
在把x∈[2k,2k+1]转化为x-2k∈[0,1],利用x∈[0,1]时F(x)=f(x)可得x∈[2k,2k+1](k∈N)时的解析式.
(3)利用转化的思想把F(x)<-x+a转化为a>1+x-
| 1 |
| x-2k+1 |
解答: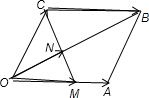 解:(1)利用平行四边形对边平行且相等以及平行线分线段成比例可得:
解:(1)利用平行四边形对边平行且相等以及平行线分线段成比例可得:
=
=
(2分),
又由
=x
,
=y
;
∴x=
,从而y=
.(4分)
(2)当x∈[0,1]时,F(x)=
.
∵F(x)图象关于直线x=1对称,
∴F(2-x)=F(x),(5分)
∴F(x+2)=F(-x),又F(x)为偶函数,
∴F(x+2)=F(x).(7分)
设x∈[2k,2k+1],则x-2k∈[0,1],(8分)
∴F(x-2k)=
,即F(x)=
.(10分)
(3)不等式为
<-x+a,(12分)
∴a>1+x-
对x∈[2k,2k+1](k∈N)恒成立,
因此a>(1+x-
)max.(14分)
∵1+x-
在x∈[2k,2k+1]上单调递增,
∴x=2k+1时其最大值为2k+
,
∴a>2k+
,即a∈(2k+
,+∞)(k∈N).(16分)
 解:(1)利用平行四边形对边平行且相等以及平行线分线段成比例可得:
解:(1)利用平行四边形对边平行且相等以及平行线分线段成比例可得:|
| ||
|
|
|
| ||
|
|
|
| ||
|
|
又由
| OM |
| OA |
| ON |
| OB |
∴x=
| y |
| 1-y |
| x |
| 1+x |
(2)当x∈[0,1]时,F(x)=
| x |
| x+1 |
∵F(x)图象关于直线x=1对称,
∴F(2-x)=F(x),(5分)
∴F(x+2)=F(-x),又F(x)为偶函数,
∴F(x+2)=F(x).(7分)
设x∈[2k,2k+1],则x-2k∈[0,1],(8分)
∴F(x-2k)=
| x-2k |
| x-2k+1 |
| x-2k |
| x-2k+1 |
(3)不等式为
| x-2k |
| x-2k+1 |
∴a>1+x-
| 1 |
| x-2k+1 |
因此a>(1+x-
| 1 |
| x-2k+1 |
∵1+x-
| 1 |
| x-2k+1 |
∴x=2k+1时其最大值为2k+
| 3 |
| 2 |
∴a>2k+
| 3 |
| 2 |
| 3 |
| 2 |
点评:本题是对向量和函数的奇偶性,单调性,对称性和恒成立问题的综合考查,是一道综合性极强的好题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
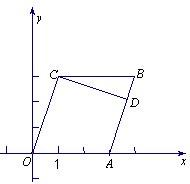 如图,在平行四边形OABC中,点C(1,3).
如图,在平行四边形OABC中,点C(1,3). 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点. 如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.
如图,在平行四边形OABC中,点O是原点,点A和点C的坐标分别是(3,0)、(1,3),点D是线段AB上的动点.