题目内容
已知函数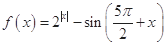 ,对于任意的
,对于任意的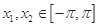 ,有如下条件:
,有如下条件:
① ; ②
; ②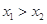 ; ③
; ③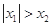 ; ④
; ④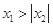 .
.
其中能使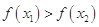 恒成立的条件序号是 .
恒成立的条件序号是 .
①④.
解析试题分析:首先原函数可化为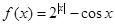 ,在
,在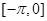 ,
,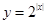 单调递减,
单调递减,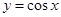 单调递增,则
单调递增,则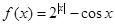 在
在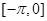 上为减函数,同理可判断
上为减函数,同理可判断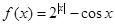 在
在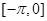 上为增函数,且可知
上为增函数,且可知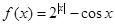 为偶函数,因此,对于①,即为
为偶函数,因此,对于①,即为
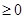
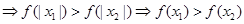 成立,对于④,由于
成立,对于④,由于
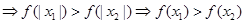 恒成立,而对于②与③,不能肯定
恒成立,而对于②与③,不能肯定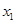 与
与 是落在定义域的正还是负区间内,所以不能保证使
是落在定义域的正还是负区间内,所以不能保证使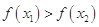 恒成立,综上所述选择①④.
恒成立,综上所述选择①④.
考点:偶函数满足: ,函数的单调性定义,化归思想.
,函数的单调性定义,化归思想.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
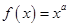 的图像经过点
的图像经过点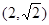 ,则
,则 的值为_________.
的值为_________. ,则使得
,则使得 成立的
成立的 的取值范围是 .
的取值范围是 .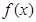 =
=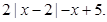 的最小值为________________.
的最小值为________________. ___________.
___________.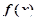 满足对任意
满足对任意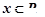 ,均有
,均有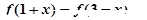 且
且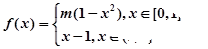 ,若方程
,若方程 恰有5个实数解,则实数
恰有5个实数解,则实数 的取值范围是 .
的取值范围是 .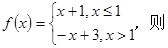 f(2) =
f(2) = x2的值域是________.
x2的值域是________.