题目内容
已知函数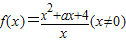 .
.(1)若f(x)为奇函数,求a的值;
(2)若f(x)在[3,+∞)上恒大于0,求a的取值范围.
【答案】分析:(1)根据奇函数对应的关系式f(-x)=-f(x),列出方程化简后求出a的值;
(2)由函数的解析式求出导数,根据导数的解析式和区间[3,+∞),判断出f′(x)>0,进而判断出函数的单调性,求出函数的最小值,只要此最小值大于0即可.
解答:解:(1)由题意知,f(x)的定义域关于原点对称,
若f(x)为奇函数,则 ,
,
即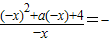
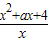 ,解得a=0.
,解得a=0.
(2)由f(x)=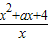 得,
得, ,
,
∴在[3,+∞)上f′(x)>0,∴f(x)在[3,+∞)上单调递增,
∴f(x)在[3,+∞)上恒大于0只要f(3)大于0即可,即3a+13>0,解得 ,
,
故a的取值范围为 .
.
点评:本题是有关函数的综合题,利用函数的奇偶性的关系式进行求值,利用函数的导数的符号判断函数的单调性,进而求出函数的最值,解决恒成立问题,考查了转化思想和逻辑思维能力.
(2)由函数的解析式求出导数,根据导数的解析式和区间[3,+∞),判断出f′(x)>0,进而判断出函数的单调性,求出函数的最小值,只要此最小值大于0即可.
解答:解:(1)由题意知,f(x)的定义域关于原点对称,
若f(x)为奇函数,则
 ,
,即
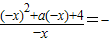
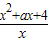 ,解得a=0.
,解得a=0.(2)由f(x)=
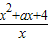 得,
得, ,
,∴在[3,+∞)上f′(x)>0,∴f(x)在[3,+∞)上单调递增,
∴f(x)在[3,+∞)上恒大于0只要f(3)大于0即可,即3a+13>0,解得
 ,
,故a的取值范围为
 .
.点评:本题是有关函数的综合题,利用函数的奇偶性的关系式进行求值,利用函数的导数的符号判断函数的单调性,进而求出函数的最值,解决恒成立问题,考查了转化思想和逻辑思维能力.

练习册系列答案
相关题目
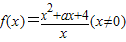 .
. .
. .
. .
. .
.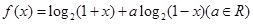 .
. .
.