题目内容
已知等差数列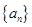 的前三项依次为
的前三项依次为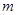 、4、
、4、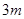 ,前
,前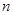 项和为
项和为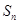 ,且
,且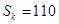 .
.
(1)求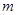 及
及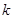 的值;
的值;
(2)设数列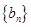 的通项
的通项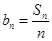 ,证明数列
,证明数列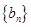 是等差数列,并求其前
是等差数列,并求其前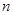 项和
项和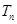 .
.
【答案】
(1)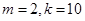 ;(2)
;(2)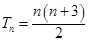 .
.
【解析】
试题分析:(1)等差数列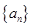 的前三项依次为
的前三项依次为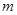 、4、
、4、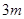 ,由等差中项性质可求出
,由等差中项性质可求出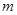 ,从而得到前
,从而得到前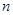 项和为
项和为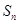 ,再由
,再由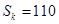 即可求出
即可求出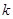 的值;(2)由
的值;(2)由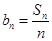 ,可得
,可得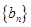 的通项公式,从而得出
的通项公式,从而得出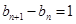 ,即证明了数列
,即证明了数列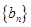 是等差数列,再由等差数列前
是等差数列,再由等差数列前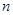 项和可以求出
项和可以求出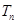 .
.
试题解析:(1)等差数列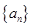 的前三项依次为
的前三项依次为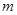 、4、
、4、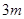 ,所以4是
,所以4是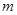 、
、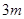 的等差中项,
的等差中项,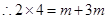 ,
,
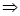
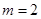 .所以等差数列的前三项依次为2、4、6,所以首项
.所以等差数列的前三项依次为2、4、6,所以首项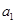 为2,公差为2.所以等差数列
为2,公差为2.所以等差数列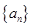 前
前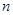 项和
项和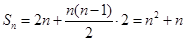 .由
.由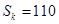 得
得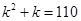 ,又
,又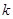 为正整数,
为正整数,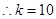 . 7分
. 7分
(2)由上问得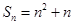 ,
,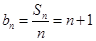 ,
, ,所以
,所以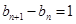 ,数列
,数列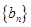 是等差数列 9分
是等差数列 9分
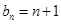 ,
,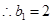 ,由等差数列前
,由等差数列前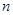 项和公式,
项和公式,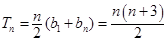 . 14分
. 14分
考点:1.等差中项性质;2.等差数列前 项和;3.等差数列的定义.
项和;3.等差数列的定义.

练习册系列答案
相关题目
 的前三项依次为
的前三项依次为 ,
, ,
, ,则
,则 .
. 的前三项为
的前三项为 ,则此数列的通项公式为______ .
,则此数列的通项公式为______ .