题目内容
(2012•辽宁)选修4-5:不等式选讲
已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|-2≤x≤1}.
(Ⅰ)求a的值;
(Ⅱ)若|f(x)-2f(
)|≤k恒成立,求k的取值范围.
已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|-2≤x≤1}.
(Ⅰ)求a的值;
(Ⅱ)若|f(x)-2f(
| x | 2 |
分析:(Ⅰ)先解不等式|ax+1|≤3,再根据不等式f(x)≤3的解集为{x|-2≤x≤1},分类讨论,即可得到结论.
(Ⅱ)记h(x)=f(x)-2f(
),从而h(x)=
,求得|h(x)|≤1,即可求得k的取值范围.
(Ⅱ)记h(x)=f(x)-2f(
| x |
| 2 |
|
解答:解:(Ⅰ)由|ax+1|≤3得-4≤ax≤2
∵不等式f(x)≤3的解集为{x|-2≤x≤1}.
∴当a≤0时,不合题意;
当a>0时,-
≤x≤
,∴a=2;
(Ⅱ)记h(x)=f(x)-2f(
),∴h(x)=
∴|h(x)|≤1
∵|f(x)-2f(
)|≤k恒成立,∴k≥1.
∵不等式f(x)≤3的解集为{x|-2≤x≤1}.
∴当a≤0时,不合题意;
当a>0时,-
| 4 |
| a |
| 2 |
| a |
(Ⅱ)记h(x)=f(x)-2f(
| x |
| 2 |
|
∴|h(x)|≤1
∵|f(x)-2f(
| x |
| 2 |
点评:本题考查绝对值不等式的解法,考查恒成立问题,将绝对值符号化去是关键,属于中档题.

练习册系列答案
相关题目
 (2012•辽宁模拟)选修4-1:几何证明选讲
(2012•辽宁模拟)选修4-1:几何证明选讲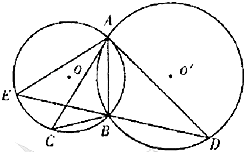 (2012•辽宁)选修4-1:几何证明选讲
(2012•辽宁)选修4-1:几何证明选讲 (2012•辽宁)选修4-1:几何证明选讲
(2012•辽宁)选修4-1:几何证明选讲