题目内容
己知等比数列{an}的公比为q,前n项和为Sn,且S1,S3,S2成等差数列.(I)求公比q;
(Ⅱ)若
 ,,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由.
,,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由.
【答案】分析:(Ⅰ)本题先根据等比数列的通项公式得a2=a1q,a3=a1q2;进而由前n项和的意义可表示出S1=a1,S2=a1+a1q,S3=a1+a1q+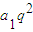 ,再利用等差数列的意义可得2S3=S1+S2,于是 2(a1+a1q+
,再利用等差数列的意义可得2S3=S1+S2,于是 2(a1+a1q+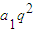 )=a1+(a1+a1q),由此方程不难求出公比q=
)=a1+(a1+a1q),由此方程不难求出公比q=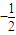 ;
;
(Ⅱ)由等比数列的通项公式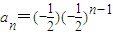 =
= ,于是
,于是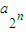 =
=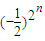 =
= ,进而可求出
,进而可求出 =
=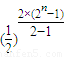 =
=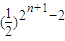 ,再根据指数函数的单调性求出其最大值.
,再根据指数函数的单调性求出其最大值.
解答:解:(Ⅰ)∵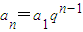 ,∴a2=a1q,
,∴a2=a1q,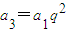 .
.
∴S1=a1,S2=a1+a1q, .
.
又∵S1,S3,S2成等差数列,
∴2S3=S1+S2,∴2(a1+a1q+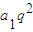 )=a1+(a1+a1q),
)=a1+(a1+a1q),
∵a1≠0,∴2(1+q+q2)=2+q,∴2q2+q=0,
又∵q≠0,∴ .
.
(Ⅱ)∵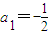 ,q=
,q=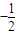 ,
,
∴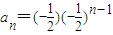 =
=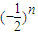 ,
,
∴ =
= =
=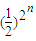 ,
,
∴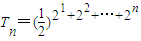 =
= =
=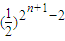 ,
,
∵2n+1-2≥2,
∴Tn≤T1=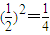 .
.
所以数列{Tn}的最大值为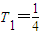 .
.
点评:本题要求学生熟练掌握等差数列、等比数列的通项公式及前n项和公式,并进行有关计算.同时会根据指数函数类型的单调性求最值.
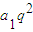 ,再利用等差数列的意义可得2S3=S1+S2,于是 2(a1+a1q+
,再利用等差数列的意义可得2S3=S1+S2,于是 2(a1+a1q+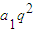 )=a1+(a1+a1q),由此方程不难求出公比q=
)=a1+(a1+a1q),由此方程不难求出公比q=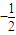 ;
;(Ⅱ)由等比数列的通项公式
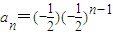 =
= ,于是
,于是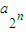 =
=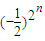 =
= ,进而可求出
,进而可求出 =
=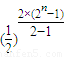 =
=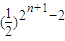 ,再根据指数函数的单调性求出其最大值.
,再根据指数函数的单调性求出其最大值.解答:解:(Ⅰ)∵
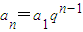 ,∴a2=a1q,
,∴a2=a1q,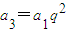 .
.∴S1=a1,S2=a1+a1q,
 .
.又∵S1,S3,S2成等差数列,
∴2S3=S1+S2,∴2(a1+a1q+
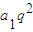 )=a1+(a1+a1q),
)=a1+(a1+a1q),∵a1≠0,∴2(1+q+q2)=2+q,∴2q2+q=0,
又∵q≠0,∴
 .
.(Ⅱ)∵
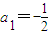 ,q=
,q=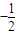 ,
,∴
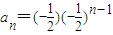 =
=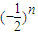 ,
,∴
 =
= =
=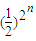 ,
,∴
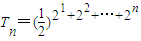 =
= =
=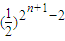 ,
,∵2n+1-2≥2,
∴Tn≤T1=
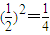 .
.所以数列{Tn}的最大值为
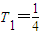 .
.点评:本题要求学生熟练掌握等差数列、等比数列的通项公式及前n项和公式,并进行有关计算.同时会根据指数函数类型的单调性求最值.

练习册系列答案
相关题目
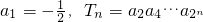 ,,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由.
,,问数列{Tn}是否存在最大项?若存在,求出该项的值;若不存在,请说明理由.