题目内容
已知定点C(-1,0)及椭圆x2+3y2=5,过点C的动直线与椭圆相交于A,B两点.(Ⅰ)若线段AB中点的横坐标是-
| 1 |
| 2 |
(Ⅱ)在x轴上是否存在点M,使
| MA |
| MB |
分析:(1)根据题意,设出直线AB的方程,将直线方程代入椭圆,用设而不求韦达定理方法表示出中点坐标,此时代入已知AB中点的横坐标即可求出直线AB的方程.
(2)假设存在点M,使
•
为常数.分别分当直线AB与x轴不垂直时以及当直线AB与x轴垂直时求出点M的坐标.最后综合两种情况得出结论.
(2)假设存在点M,使
| MA |
| MB |
解答:解:(Ⅰ)依题意,直线AB的斜率存在,设直线AB的方程为y=k(x+1),
将y=k(x+1)代入x2+3y2=5,消去y整理得(3k2+1)x2+6k2x+3k2-5=0.
设A(x1,y1),B(x2,y2),则
由线段AB中点的横坐标是-
,得
=-
=-
,
解得k=±
,适合(1).
所以直线AB的方程为x-
y+1=0,或x+
y+1=0.
(Ⅱ)解:假设在x轴上存在点M(m,0),使
•
为常数.
①当直线AB与x轴不垂直时,由(Ⅰ)知x1+x2=-
,x1x2=
.(3)
所以
•
=(x1-m)(x2-m)+y1y2=(x1-m)(x2-m)+k2(x1+1)(x2+1)
=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2
将(3)代入,整理得
•
=
+m2=
+m2
=m2+2m-
-
.
注意到
•
是与k无关的常数,从而有6m+14=0,m=-
,此时
•
=
.
②当直线AB与x轴垂直时,此时点A,B的坐标分别为(-1,
)、(-1,-
),
当m=-
时,亦有
•
=
.
综上,在x轴上存在定点M(-
,0),使
•
为常数.
将y=k(x+1)代入x2+3y2=5,消去y整理得(3k2+1)x2+6k2x+3k2-5=0.
设A(x1,y1),B(x2,y2),则
|
由线段AB中点的横坐标是-
| 1 |
| 2 |
| x1+x2 |
| 2 |
| 3k2 |
| 3k2+1 |
| 1 |
| 2 |
解得k=±
| ||
| 3 |
所以直线AB的方程为x-
| 3 |
| 3 |
(Ⅱ)解:假设在x轴上存在点M(m,0),使
| MA |
| MB |
①当直线AB与x轴不垂直时,由(Ⅰ)知x1+x2=-
| 6k2 |
| 3k2+1 |
| 3k2-5 |
| 3k2+1 |
所以
| MA |
| MB |
=(k2+1)x1x2+(k2-m)(x1+x2)+k2+m2
将(3)代入,整理得
| MA |
| MB |
| (6m-1)k2-5 |
| 3k2+1 |
(2m-
| ||||
| 3k2+1 |
=m2+2m-
| 1 |
| 3 |
| 6m+14 |
| 3(3k2+1) |
注意到
| MA |
| MB |
| 7 |
| 3 |
| MA |
| MB |
| 4 |
| 9 |
②当直线AB与x轴垂直时,此时点A,B的坐标分别为(-1,
| 2 | ||
|
| 2 | ||
|
当m=-
| 7 |
| 3 |
| MA |
| MB |
| 4 |
| 9 |
综上,在x轴上存在定点M(-
| 7 |
| 3 |
| MA |
| MB |
点评:本题考查直线的一般方程以及直线与圆锥曲线的关系求法.通过运用设而不求韦达定理方法,以及向量垂直关系的利用求解.考查对知识的综合运用,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
|
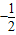 ,求直线AB的方程;
,求直线AB的方程;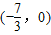 ,求
,求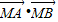 的值.
的值.