题目内容
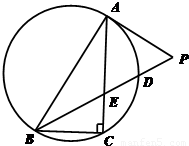
如图所示,D是Rt△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.
(1)证明sinα+cos2β=0;
(2)若AC=![]() DC,求β的值.
DC,求β的值.
(1)证明:因为α=![]() -∠BAD=
-∠BAD=![]() -(π-2β)=2β-
-(π-2β)=2β-![]() ,
,
所以sinα=sin(2β-![]() )=-cos2β,
)=-cos2β,
即sinα+cos2β=0.
(2)解析:在△ADC中,由正弦定理得
![]() =
=![]() ,即
,即![]() =
=![]() .
.
所以sinβ=![]() sinα.
sinα.
由(1),sinα=-cos2β,
所以sinβ=-![]() cos2β=-
cos2β=-![]() (1-2sin2β),
(1-2sin2β),
即2![]() sin2β-sinβ-
sin2β-sinβ-![]() =0.
=0.
解得sinβ=![]() 或sinβ=-
或sinβ=-![]() .
.
因为0<β<![]() ,
,
所以sinβ=![]() .
.
从而β=![]() .
.

练习册系列答案
相关题目
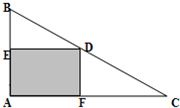 Rt△ABC如图所示,直角边|AB|=3,|AC|=4.D点是斜边BC上的动点,DE⊥AB交于点E,DF⊥AC交于点F.设|AE|=x,四边形FDEA的面积为y,求y关于x的函数
Rt△ABC如图所示,直角边|AB|=3,|AC|=4.D点是斜边BC上的动点,DE⊥AB交于点E,DF⊥AC交于点F.设|AE|=x,四边形FDEA的面积为y,求y关于x的函数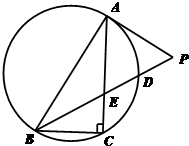 (2012•丰台区一模)如图所示,Rt△ABC内接于圆,∠ABC=60°,PA是圆的切线,A为切点,PB交AC于E,交圆于D.若PA=AE,PD=
(2012•丰台区一模)如图所示,Rt△ABC内接于圆,∠ABC=60°,PA是圆的切线,A为切点,PB交AC于E,交圆于D.若PA=AE,PD=
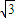 ,BD=
,BD=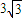 ,则AP= ,AC= .
,则AP= ,AC= .