题目内容
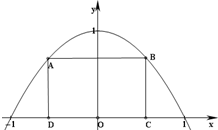
如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元,问如何规划才能使得整块土地总价值最大.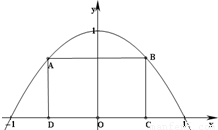
【答案】分析:先由定积分可求整个地块的面积,进而可得工业用地面积,三个边角地块面积,由此可得土地总价值,利用导数的方法可求函数的最值.
解答:解:由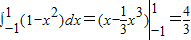 ,知整个地块的面积为
,知整个地块的面积为 …(2分)
…(2分)
设点C的坐标为(x,0),则点B(x,1-x2)其中0<x<1,
∴SABCD=2x(1-x2)…(4分)
∴土地总价值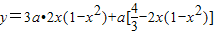
=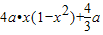 …(6分)
…(6分)
由y'=4a(1-3x2)=0得 …(8分)
…(8分)
并且当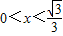 时,
时,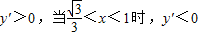
故当 时,y取得最大值. …(11分)
时,y取得最大值. …(11分)
答:当点C的坐标为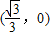 时,整个地块的总价值最大. …(12分)
时,整个地块的总价值最大. …(12分)
点评:本题以实际问题为载体,考查函数模型的构建,解题的关键是利用定积分知识求面积,从而构建函数,同时考查利用导数求最值,综合性强.
解答:解:由
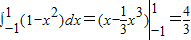 ,知整个地块的面积为
,知整个地块的面积为 …(2分)
…(2分)设点C的坐标为(x,0),则点B(x,1-x2)其中0<x<1,
∴SABCD=2x(1-x2)…(4分)
∴土地总价值
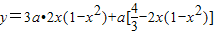
=
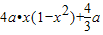 …(6分)
…(6分)由y'=4a(1-3x2)=0得
 …(8分)
…(8分)并且当
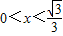 时,
时,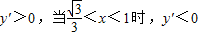
故当
 时,y取得最大值. …(11分)
时,y取得最大值. …(11分)答:当点C的坐标为
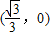 时,整个地块的总价值最大. …(12分)
时,整个地块的总价值最大. …(12分)点评:本题以实际问题为载体,考查函数模型的构建,解题的关键是利用定积分知识求面积,从而构建函数,同时考查利用导数求最值,综合性强.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元,问如何规划才能使得整块土地总价值最大.
如图所示,抛物线y=1-x2与x轴所围成的区域是一块等待开垦的土地,现计划在该区域内围出一块矩形地块ABCD作为工业用地,其中A、B在抛物线上,C、D在x轴上.已知工业用地每单位面积价值为3a元(a>0),其它的三个边角地块每单位面积价值a元,问如何规划才能使得整块土地总价值最大. (1)求使△PAB的面积最大的P点的坐标(a,b);
(1)求使△PAB的面积最大的P点的坐标(a,b); 引抛物线的切线,切点分别为A,B.
引抛物线的切线,切点分别为A,B.