题目内容
对于非零向量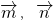 ,定义运算“#”:
,定义运算“#”: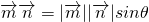 ,其中θ为
,其中θ为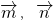 的夹角.有两两不共线的三个向量
的夹角.有两两不共线的三个向量 ,下列结论:
,下列结论:
①若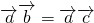 ,则
,则 ;②
;②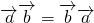 ;
;
③若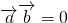 ,则
,则 ;④
;④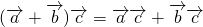 ;
;
⑤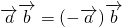 .
.
其中正确的个数有
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:严格按照定义运算“#”,逐一检验各个选项的正确性,从而得出结论.
解答:∵两两不共线的三个向量 ,∴
,∴ 不可能成立,故①不正确.
不可能成立,故①不正确.
∵ #
# =|
=| |•|
|•| |•sin<
|•sin< ,
, >,
>, •
• =|
=| |•|
|•| |•sin<
|•sin< ,
, >,故②正确.
>,故②正确.
由 #
# =|
=| |•|
|•| |•sin<
|•sin< ,
, >=0,可得 sin<
>=0,可得 sin< ,
, >=0,则
>=0,则 ; 故③正确.
; 故③正确.
( +
+ )#
)# =|
=| +
+ |•|
|•| |sin<(
|sin<( +
+ ),
), >,
>, #
# +
+ #
# =|
=| |•|
|•| |•sin<
|•sin< ,
, >+|
>+| |•|
|•| |•sin<
|•sin< ,
, >,
>,
故④不成立.
 #
# =|
=| |•|
|•| |•sin<
|•sin< ,
, >,(-
>,(- )#
)# =|-
=|- |•|
|•| |•sin<-
|•sin<- ,
, >=|
>=| |•|
|•| |•sin<
|•sin< ,
, >,
>,
故⑤正确.
综上,②③⑤正确,①④不正确.故选 C.
点评:本题考查向量的几何表示,共线向量的性质,准确把握和理解定义运算“#”的含义.
分析:严格按照定义运算“#”,逐一检验各个选项的正确性,从而得出结论.
解答:∵两两不共线的三个向量
 ,∴
,∴ 不可能成立,故①不正确.
不可能成立,故①不正确.∵
 #
# =|
=| |•|
|•| |•sin<
|•sin< ,
, >,
>, •
• =|
=| |•|
|•| |•sin<
|•sin< ,
, >,故②正确.
>,故②正确.由
 #
# =|
=| |•|
|•| |•sin<
|•sin< ,
, >=0,可得 sin<
>=0,可得 sin< ,
, >=0,则
>=0,则 ; 故③正确.
; 故③正确.(
 +
+ )#
)# =|
=| +
+ |•|
|•| |sin<(
|sin<( +
+ ),
), >,
>, #
# +
+ #
# =|
=| |•|
|•| |•sin<
|•sin< ,
, >+|
>+| |•|
|•| |•sin<
|•sin< ,
, >,
>,故④不成立.
 #
# =|
=| |•|
|•| |•sin<
|•sin< ,
, >,(-
>,(- )#
)# =|-
=|- |•|
|•| |•sin<-
|•sin<- ,
, >=|
>=| |•|
|•| |•sin<
|•sin< ,
, >,
>,故⑤正确.
综上,②③⑤正确,①④不正确.故选 C.
点评:本题考查向量的几何表示,共线向量的性质,准确把握和理解定义运算“#”的含义.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
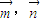 ,定义运算“#”:
,定义运算“#”: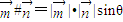 ,其中θ为
,其中θ为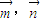 的夹角.有两两不共线的三个向量
的夹角.有两两不共线的三个向量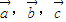 ,下列结论:
,下列结论: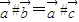 ,则
,则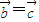 ;②
;②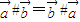 ;
;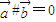 ,则
,则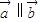 ;④
;④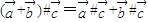 ;
;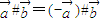 .
.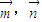 ,定义运算“#”:
,定义运算“#”: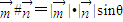 ,其中θ为
,其中θ为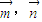 的夹角.有两两不共线的三个向量
的夹角.有两两不共线的三个向量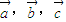 ,下列结论:
,下列结论: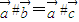 ,则
,则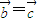 ;②
;②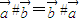 ;
;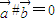 ,则
,则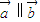 ;④
;④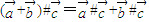 ;
;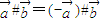 .
.