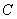题目内容
某学生参加某高校的自主招生考试,须依次参加A、B、C、D、E五项考试,如果前四项中有两项不合格或第五项不合格,则该考生就被淘汰,考试即结束;考生未被淘汰时,一定继续参加后面的考试.已知每一项测试都是相互独立的,该生参加A、B、C、D四项考试不合格的概率均为 ,参加第五项不合格的概率为
,参加第五项不合格的概率为 ,
,
(1)求该生被录取的概率;
(2)记该生参加考试的项数为X,求X的分布列和期望.
解:(1)该生被录取,则A、B、C、D四项考试答对3道或4道,并且答对第五项.
所以该生被录取的概率为P= [(
[(  )4+C
)4+C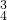 (
( )3•
)3• ]=
]= ,
,
(2)该生参加考试的项数X的所有取值为:2,3,4,5.
P(X=2)= ×
× =
= ;P(X=3)=C
;P(X=3)=C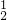 •
• •
• •
• =
= ;P(X=4)=C
;P(X=4)=C •
• •(
•(  )2•
)2• =
= ;
;
P(X=5)=1- -
- -
- =
= .
.
该生参加考试的项数ξ的分布列为:
EX=2× +3×
+3× +4×
+4× +5×
+5× =
= .
.
分析:(1)该生被录取,则必须答对前四项中的三项和第五项或者答对所有的项.
(2)分析此问题时要注意有顺序,所以X的所有取值为:2,3,4,5.分别计算其概率得出分布列,以及它的期望值.
点评:本题主要考查了离散型随机变量及其分布列,数学期望.此题把二项分布和回合制问题有机的结合在一起,增加了试题的难度.解决此问题应注意顺序.
所以该生被录取的概率为P=
 [(
[(  )4+C
)4+C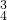 (
( )3•
)3• ]=
]= ,
,(2)该生参加考试的项数X的所有取值为:2,3,4,5.
P(X=2)=
 ×
× =
= ;P(X=3)=C
;P(X=3)=C •
• •
• •
• =
= ;P(X=4)=C
;P(X=4)=C •
• •(
•(  )2•
)2• =
= ;
;P(X=5)=1-
 -
- -
- =
= .
.该生参加考试的项数ξ的分布列为:
| X | 2 | 3 | 4 | 3 |
| P |  |  |  |  |
 +3×
+3× +4×
+4× +5×
+5× =
= .
.分析:(1)该生被录取,则必须答对前四项中的三项和第五项或者答对所有的项.
(2)分析此问题时要注意有顺序,所以X的所有取值为:2,3,4,5.分别计算其概率得出分布列,以及它的期望值.
点评:本题主要考查了离散型随机变量及其分布列,数学期望.此题把二项分布和回合制问题有机的结合在一起,增加了试题的难度.解决此问题应注意顺序.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某市 四所中学报名参加某高校今年自主招生的学生人数如下表所示:
四所中学报名参加某高校今年自主招生的学生人数如下表所示:
中学 | | | | |
人数 | | | | |
为了了解参加考试的学生的学习状况,该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查.
(1)问 四所中学各抽取多少名学生?
四所中学各抽取多少名学生?
(2)从参加问卷调查的 名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;
名学生中随机抽取两名学生,求这两名学生自同一所中学的概率;
(3)在参加问卷调查的 名学生中,从自
名学生中,从自 两所中学的学生当中随机抽取两名学
两所中学的学生当中随机抽取两名学
生,用 表示抽得
表示抽得 中学的学生人数,求
中学的学生人数,求 的分布列和期望.
的分布列和期望.