题目内容
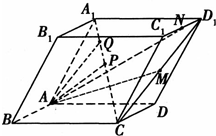 如图所示,在各个面都是平行四边形的四棱柱ABCD-A1B1C1D1中,P是CA1的中点,M是CD1的中点,N是C1D1的中点,点Q在CA1上,且CQ:QA1=4:1,设
如图所示,在各个面都是平行四边形的四棱柱ABCD-A1B1C1D1中,P是CA1的中点,M是CD1的中点,N是C1D1的中点,点Q在CA1上,且CQ:QA1=4:1,设| AB |
| AD |
| AA1 |
(1)
| AP |
(2)
| AM |
(3)
| AN |
(4)
| AQ |
分析:利用向量的平行四边形法则和向量的共线定理即可得出.
解答:解:如图所示,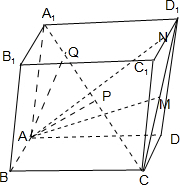
(1)
=
(
+
)=
(
+
+
)=
(
+
+
);
(2)
=
(
+
)=
(
+2
+
)=
(
+2
+
);
(3)
=
(
+
)=
[(
+
+
)+(
+
)]
=
(
+2
+2
)=
+
+
;
(4)
=
+
=
+
=
+
(
-
)
=
+
=
(
+
)+
=
+
+
.

(1)
| AP |
| 1 |
| 2 |
| AC |
| AA1 |
| 1 |
| 2 |
| AB |
| AD |
| AA1 |
| 1 |
| 2 |
| a |
| b |
| c |
(2)
| AM |
| 1 |
| 2 |
| AC |
| AD1 |
| 1 |
| 2 |
| AB |
| AD |
| AA1 |
| 1 |
| 2 |
| a |
| b |
| c |
(3)
| AN |
| 1 |
| 2 |
| AC1 |
| AD1 |
| 1 |
| 2 |
| AB |
| AD |
| AA1 |
| AD |
| AA1 |
=
| 1 |
| 2 |
| AB |
| AD |
| AA1 |
| 1 |
| 2 |
| a |
| b |
| c |
(4)
| AQ |
| AC |
| CQ |
| AC |
| 4 |
| 5 |
| CA1 |
| AC |
| 4 |
| 5 |
| AA1 |
| AC |
=
| 1 |
| 5 |
| AC |
| 4 |
| 5 |
| AA1 |
| 1 |
| 5 |
| AB |
| AD |
| 4 |
| 5 |
| AA1 |
| 1 |
| 5 |
| a |
| 1 |
| 5 |
| b |
| 4 |
| 5 |
| c |
点评:熟练掌握向量的平行四边形法则和向量的共线定理是解题的关键.

练习册系列答案
相关题目
 ,用基底{a,b,c}表示以下向量:
,用基底{a,b,c}表示以下向量: ;
; ;
; ;
;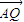 .
.