题目内容
已知定义在 上的奇函数
上的奇函数 ,满足
,满足 ,且在区间
,且在区间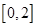 上是增函数,若方程
上是增函数,若方程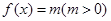 ,在区间
,在区间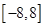 上有四个不同的根
上有四个不同的根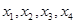 ,则
,则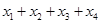 =( )
=( )
| A.-12 | B.-8 | C.-4 | D.4 |
B
解析试题分析:因为定义在 上的奇函数,满足
上的奇函数,满足 ,所以
,所以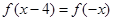 ,所以, 由
,所以, 由 为奇函数,所以函数图象关于直线
为奇函数,所以函数图象关于直线 对称且
对称且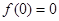 ,由
,由 知
知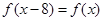 ,所以函数是以8为周期的周期函数,又因为
,所以函数是以8为周期的周期函数,又因为 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以 在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间
在区间[-2,0]上也是增函数.如图所示,那么方程f(x)=m(m>0)在区间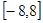 上有四个不同的根
上有四个不同的根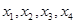 ,不妨设
,不妨设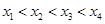 由对称性知
由对称性知 ,
,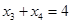 ,所以
,所以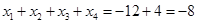 .
.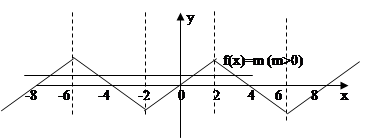
考点:1.函数的奇偶性与单调性;2.方程与函数的综合应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知定义在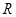 上的偶函数
上的偶函数 满足
满足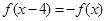 且在区间
且在区间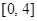 上是增函数则( )
上是增函数则( )
A.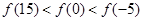 | B.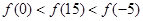 |
C.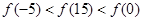 | D.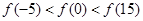 |
函数 的定义域是( )
的定义域是( )
A. | B. | C. | D. |
己知函数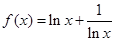 ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.若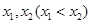 是 是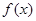 的极值点,则 的极值点,则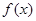 在区间 在区间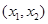 内是增函数 内是增函数 |
B.若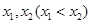 是 是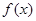 的极值点,则 的极值点,则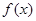 在区间 在区间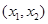 内是减函数 内是减函数 |
C.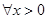 ,且 ,且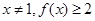 |
D. , ,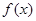 在 在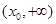 上是增函数 上是增函数 |
定义运算 ,若函数
,若函数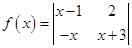 在
在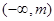 上单调递减,则实数
上单调递减,则实数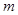 的取值范围是( )
的取值范围是( )
A.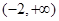 | B.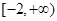 | C.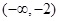 | D.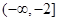 |
已知定义域为R的函数f(x)在区间(8,+∞)上为减函数,且函数y=f(x+8)为偶函数,则
| A.f(6)>f(7) | B.f(6)>f(9) |
| C.f(7)>f(9) | D.f(7)>f(10) |
 的图像可能是( )
的图像可能是( )

 ,则函数图像可能是( )
,则函数图像可能是( )