题目内容
函数y=2sin(2x- )的一条对称轴是 ( )
)的一条对称轴是 ( )
A.x=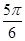 | B.x= | C.x=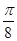 , , | D.x=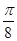 |
C
解析试题分析:函数图象的对称轴,经过函数图象的最高点或最低点。
所以,由2x- =
=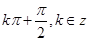 ,得,
,得,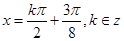 ,x=
,x=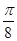 是一条对称轴,故选C。
是一条对称轴,故选C。
考点:本题主要考查正弦型函数的图象和性质。
点评:简单题,函数图象的对称轴,经过函数图象的最高点或最低点。

练习册系列答案
相关题目
函数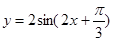 的图像 ( )
的图像 ( )
| A.关于原点对称 | B.关于点(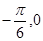 )对称 )对称 |
| C.关于y轴对称 | D.关于直线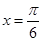 对称 对称 |
若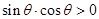 ,则
,则 在( )
在( )
| A.第一、二象限 | B.第一、三象限 |
| C.第一、四象限 | D.第二、四象限 |
若点P(sinα-cosα,tanα)在第一象限,则在[0,2p)内α的取值范围是 ( )
A.( , ,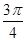 )∪(p, )∪(p,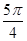 ) ) | B.( , , )∪(p, )∪(p,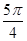 ) ) |
C.( , ,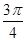 )∪( )∪(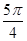 , ,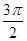 ) ) | D.( , ,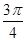 )∪( )∪(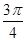 ,p) ,p) |
右图是函数 在区间
在区间 上的图象.为了得到这个函数的图象,只需将
上的图象.为了得到这个函数的图象,只需将 的图象上所有的点
的图象上所有的点
A.向左平移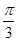 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的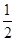 倍,纵坐标不变 倍,纵坐标不变 |
B.向左平移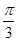 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
C.向左平移 个单位长度,再把所得各点的横坐标缩短到原来的 个单位长度,再把所得各点的横坐标缩短到原来的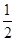 倍,纵坐标不变 倍,纵坐标不变 |
D.向左平移 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变 |
如图所示,是函数y=Asin(ωx+φ)(A>0,ω>0, -p<φ<0)的简图,则振幅、周期、初相分别是 ( )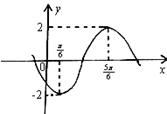
A.2, ,? ,? | B.2, ,? ,?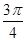 |
C.4, ,? ,?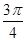 | D.2,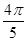 ,? ,? |
已知 ,则
,则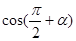 的值为( )
的值为( )
A.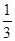 | B.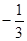 | C.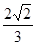 | D. |
下列能使cosθ<sinθ<tanθ成立的θ所在区间是( )
A. | B. | C. | D.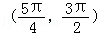 |
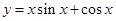 的图象上的点
的图象上的点 处的切线的斜率为k,若
处的切线的斜率为k,若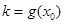 ,则函数
,则函数