题目内容
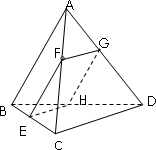
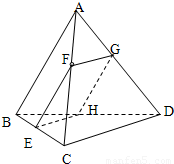
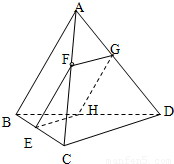
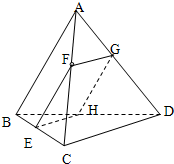 如图,在棱长都等于1的三棱锥A-BCD中,F是AC上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H.
如图,在棱长都等于1的三棱锥A-BCD中,F是AC上的一点,过F作平行于棱AB和棱CD的截面,分别交BC,AD,BD于E,G,H.(1)证明截面EFGH是矩形;
(2)F在AC的什么位置时,截面面积最大,说明理由.
分析:(1)根据面面平行的性质定理,可得AB∥EF,AB∥GH,进而EF∥GH,同理EH∥CD∥FG,则可得四边形EFGH是平行四边形,结合四棱锥的几何特征,证得EF⊥CD后,可得截面EFGH是矩形;
(2)设FG=x,x∈(0,1),可得四边形面积的解析式:SEFGH=EF•FG=x(1-x),进而根据二次函数的图象和性质,可得答案.
(2)设FG=x,x∈(0,1),可得四边形面积的解析式:SEFGH=EF•FG=x(1-x),进而根据二次函数的图象和性质,可得答案.
解答:证明:(1)∵AB∥平面EFGH,
平面ABC∩平面EFGH=EF
∴AB∥EF
同理AB∥GH
∴EF∥GH
同理EH∥CD∥FG
∴四边形EFGH是平行四边形
取CD中点S,连接AS,BS
∵AC=AD,S是CD中点
∴AS⊥CD
同理 BS⊥CD
又∵AS∩BS=S
∴CD⊥平面ABS
∴CD⊥AB
又∵AB∥EF,FG∥CD
∴EF⊥CD
即 四边形EFGH是矩形
解:(2)设FG=x,x∈(0,1)
由(1)知
=
=
,
又CD=AB=1
∴EF=1-x
则SEFGH=EF•FG=x(1-x)
=-(x-
)2+
∴当x=
时,SEFGH最大
即F是AC的中点时,截面面积最大
平面ABC∩平面EFGH=EF
∴AB∥EF
同理AB∥GH
∴EF∥GH
同理EH∥CD∥FG
∴四边形EFGH是平行四边形
取CD中点S,连接AS,BS
∵AC=AD,S是CD中点
∴AS⊥CD
同理 BS⊥CD
又∵AS∩BS=S
∴CD⊥平面ABS
∴CD⊥AB
又∵AB∥EF,FG∥CD
∴EF⊥CD
即 四边形EFGH是矩形
解:(2)设FG=x,x∈(0,1)
由(1)知
| FG |
| CD |
| AF |
| AC |
| AB-EF |
| AB |
又CD=AB=1
∴EF=1-x
则SEFGH=EF•FG=x(1-x)
=-(x-
| 1 |
| 2 |
| 1 |
| 4 |
∴当x=
| 1 |
| 2 |
即F是AC的中点时,截面面积最大
点评:本题考查的知识点是棱锥的结构特征,特殊四边形的判定,二次函数的图象和性质,熟练掌握棱锥的结构特征是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
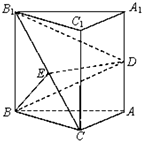 如图,在棱长都等于1的三棱柱ABC-A1B1C1中,BB1⊥平面ABC,D、E分别为AA1、B1C的中点.
如图,在棱长都等于1的三棱柱ABC-A1B1C1中,BB1⊥平面ABC,D、E分别为AA1、B1C的中点.