题目内容
双曲线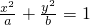 的焦点在y轴上,且a∈{-3,-2,-1,1,2},b∈{-2,-1,1,2,3,4},则不同双曲线的条数是
的焦点在y轴上,且a∈{-3,-2,-1,1,2},b∈{-2,-1,1,2,3,4},则不同双曲线的条数是
- A.C51C71
- B.C21C21
- C.C31C41
- D.C122
C
分析:根据双曲线的标准方程,易得a<0,b>0,进而由a∈{-3,-2,-1,1,2},b∈{-2,-1,1,2,3,4},可得a、b的取法数目,进而由计数原理,计算可得答案.
解答:根据题意,双曲线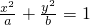 的焦点在y轴上,则a<0,b>0;
的焦点在y轴上,则a<0,b>0;
a∈{-3,-2,-1,1,2},a有C31种取法,
b∈{-2,-1,1,2,3,4},b有C41种取法,
由分步计数原理,可得不同双曲线的条数是C31C41
故选C.
点评:本题考查组合的应用,涉及双曲线的标准方程,难度不大.
分析:根据双曲线的标准方程,易得a<0,b>0,进而由a∈{-3,-2,-1,1,2},b∈{-2,-1,1,2,3,4},可得a、b的取法数目,进而由计数原理,计算可得答案.
解答:根据题意,双曲线
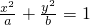 的焦点在y轴上,则a<0,b>0;
的焦点在y轴上,则a<0,b>0;a∈{-3,-2,-1,1,2},a有C31种取法,
b∈{-2,-1,1,2,3,4},b有C41种取法,
由分步计数原理,可得不同双曲线的条数是C31C41
故选C.
点评:本题考查组合的应用,涉及双曲线的标准方程,难度不大.

练习册系列答案
相关题目
中心在坐标原点,离心率为
的双曲线的焦点在y轴上,则它的渐近线方程为( )
| 5 |
| 3 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|