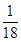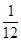题目内容

一袋中装有4个形状、大小完全相同的球，其中黑球2个，白球2个，假设每个小球从袋中被取出的可能性相同，首相由甲取出2个球，并不在将他们原袋中，然后由乙取出剩下的2个球.规定取出一个黑球记1分，取出一个白球记2分，取出球的总积分多者获胜.
（1）求甲、乙平局的概率；
（2）假设可以选择取球的先后顺序，应选择先取，还是后取，请说明理由.
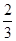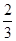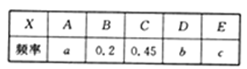
（1）；（2）先取后取获胜的可能性都一样，详细理由见解析.

试题分析：（1）不妨记黑球为1,2号；白球为3,4号，则甲取球的所有可能共有下列6种情况：12,13,14,23,24,34,其中平局得分应该是3分，所以，甲甲应取黑白小球各一个，共4种情况.故平局的概率为 . 
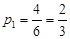（2）甲获胜时，得分只能是4分，即取出的2个白球，于是，甲（先取者）获胜的概率为所以，乙获胜的概率为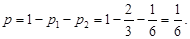 所以，先取后取获胜的可能性都一样.
（1）记黑球为1,2号；白球为3,4号.则甲取球的所有可能共有下列6种情况：12,13,14,23,24,34,平局时甲乙两人的得分应该为3分，所以，甲应取黑白小球各一个，共4种情况.故平局的概率为 . 
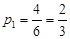（2）甲获胜时，得分只能是4分，即取出的2个白球，于是，甲（先取者）获胜的概率为所以，乙获胜的概率为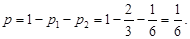 所以，先取后取获胜的可能性都一样.          
练习册系列答案
相关题目
某中学在高一开设了数学史等4门不同的选修课，每个学生必须选修，且只能从中选一门。该校高一的3名学生甲、乙、丙对这4门不同的选修课的兴趣相同。
（1）求恰有2门选修课这3个学生都没有选择的概率；
（2）设随机变量为甲、乙、丙这三个学生选修数学史这门课的人数，求的分布列及期望，方差．
对一批共50件的某电器进行分类检测，其重量（克）统计如下：
重量段
[80，85）
[85，90）
[90，95）
[95，100]
件数
5
a
15
b
规定重量在82克及以下的为“A”型，重量在85克及以上的为“B”型，已知该批电器有“A”型2件
（1）从该批电器中任选1件，求其为“B”型的概率；
（2）从重量在［80,85)的5件电器中，任选2件，求其中恰有1件为“A”型的概率.
甲，乙两名运动员各自等可能地从红、白、蓝3种颜色的运动服中选择1种，则他们选择相同颜色运动服的概率为_______．
某人把大小相同的3个黄色，3个白色的乒乓球放到一个盒子里，让人摸球。规定：若摸得同色3个球，则送给摸球者5元钱，若摸得非同色的3个球，摸球者付给自己1元钱。假定一天内有100人次摸球，试从概率角度估算一下这个人一年（按360天计算）能赚的钱数为（   ）
A．6000B．12000C．7200D．14400
从中随机选取一个数为从中随机选取一个数，则的概率是（　　）
A．B．C．D．
袋中有2个红球，2个蓝球，1个白球，从中一次取出2个球，则取出的球颜色相同的概率为   ．
某食品厂对生产的某种食品按行业标准分成五个不同等级，等级系数X依次为A，B，C，D,E．现从该种食品中随机抽取20件样品进行检验，对其等级系数进行统计分析，得到频率分布表如下：

(1)在所抽取的20件样品中，等级系数为D的恰有3件，等级系数为E的恰有2件，求a,b,c的值；
(2)在（1)的条件下，将等级系数为D的3件样品记为x1，x2，x3，等级系数为E的2件样品记为y1，y2，现从x1，x2，x3，y1，y2这5件样品中一次性任取两件（假定每件样品被取出的可能性相同），试写出所有可能的结果，并求取出的两件样品是同一等级的概率．
同时投掷两个骰子，则向上的点数之差的绝对值为4的概率是（  ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网