题目内容
已知0<x<(1)若tan![]() =
=![]() ,分别求出cosx、cosy的值;
,分别求出cosx、cosy的值;
(2)试比较siny与sin(x+y)的大小,并说明理由.
解:(1)∵0<x<![]() <y<π,
<y<π,
又tan![]() =
=![]() ,
,
∴0<![]() <
<![]() ,
,
∴cos![]() =
=![]() ,sin
,sin![]() =
=![]() ,
,
∴cosx=2cos2![]() -1=
-1=![]() ,
,
sinx=![]() .
.
又∵sin(x+y)=![]() ,
,![]() <x+y<
<x+y<![]() .
.
∴cos(x+y)=-![]() .
.
∴cosy=cos[(x+y)-x]
=cos(x+y)cosx+sin(x+y)·sinx
=![]() ·
·![]() +
+![]() ·
·![]() =
=![]() .
.
(2)∵0<x<![]() <y<π,
<y<π,
∴![]() <x+y<
<x+y<![]() ,
,![]() <y<x+y<
<y<x+y<![]() .
.
又∵y=sinx在[![]() ,
,![]() ]上为减函数,
]上为减函数,
∴siny>sin(x+y).

练习册系列答案
相关题目
 <y<π且sin(x+y)=
<y<π且sin(x+y)=
 =
= ,分别求cosx及cosy的值;
,分别求cosx及cosy的值; <y<π且sin(x+y)=
<y<π且sin(x+y)=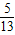
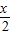 =
= ,分别求cosx及cosy的值;
,分别求cosx及cosy的值;