题目内容
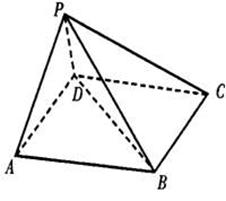
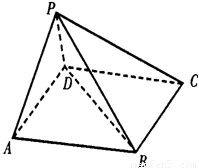
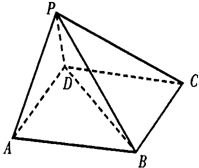 如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=
如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB= ,PD=
,PD= .
.
(1)求证:BD⊥平面PAD;
(2)若PD与底面ABCD成60°的角,试求二面角P-BC-A的大小.
解 (1)由已知AB=4,AD=2,∠BAD=60°,
得BD2=AD2+AB2-2AD•ABcos60°=4+16-2×2×4× =12.
=12.
∴AB2=AD2+BD2,∴△ABD是直角三角形,
∠ADB=90°,即AD⊥BD.
在△PDB中,PD= ,PB=
,PB= ,BD=
,BD= ,
,
∴PB2=PD2+BD2,故得PD⊥BD.
又PD∩AD=D,∴BD⊥平面PAD.
(2)∵BD⊥平面PAD,BD?平面ABCD,
∴平面PAD⊥平面ABCD.
作PE⊥AD于E,又PE?平面PAD,∴PE⊥平面ABCD,
∴∠PDE是PD与底面BCD所成的角,∴∠PDE=60°,
∴PE=PDsin60°= •
• =
=
作EF⊥BC于F,连PF,则PF⊥BC,∴∠PFE是二面角P-BC-A的平面角.
又EF=BD= ,∴在Rt△PEF中,
,∴在Rt△PEF中,
tan∠PFE=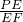 =
= =
= .
.
故二面角P-BC-A的大小为arctan .
.
分析:(1)证明直线与平面垂直,关键要找到两条相交直线与之都垂直.本小问利用勾股定理的逆定理可证得AD⊥BD,PD⊥BD,从而证出BD⊥平面PAD;
(2)作PE⊥AD于E,证出∠PDE是PD与底面BCD所成的角,再作EF⊥BC于F,连PF,则PF⊥BC,∴∠PFE是二面角P-BC-A的平面角.在Rt△PEF中,求∠PFE.
点评:本小题主要考查空间线面关系、二面角的度量,考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力
得BD2=AD2+AB2-2AD•ABcos60°=4+16-2×2×4×
 =12.
=12.∴AB2=AD2+BD2,∴△ABD是直角三角形,
∠ADB=90°,即AD⊥BD.
在△PDB中,PD=
 ,PB=
,PB= ,BD=
,BD= ,
,∴PB2=PD2+BD2,故得PD⊥BD.
又PD∩AD=D,∴BD⊥平面PAD.
(2)∵BD⊥平面PAD,BD?平面ABCD,
∴平面PAD⊥平面ABCD.
作PE⊥AD于E,又PE?平面PAD,∴PE⊥平面ABCD,
∴∠PDE是PD与底面BCD所成的角,∴∠PDE=60°,
∴PE=PDsin60°=
 •
• =
=
作EF⊥BC于F,连PF,则PF⊥BC,∴∠PFE是二面角P-BC-A的平面角.
又EF=BD=
 ,∴在Rt△PEF中,
,∴在Rt△PEF中,tan∠PFE=
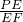 =
= =
= .
.故二面角P-BC-A的大小为arctan
 .
.分析:(1)证明直线与平面垂直,关键要找到两条相交直线与之都垂直.本小问利用勾股定理的逆定理可证得AD⊥BD,PD⊥BD,从而证出BD⊥平面PAD;
(2)作PE⊥AD于E,证出∠PDE是PD与底面BCD所成的角,再作EF⊥BC于F,连PF,则PF⊥BC,∴∠PFE是二面角P-BC-A的平面角.在Rt△PEF中,求∠PFE.
点评:本小题主要考查空间线面关系、二面角的度量,考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
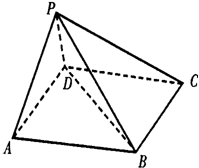 如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=
如图,在五面体P-ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,PB=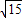 ,PD=
,PD=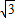 .
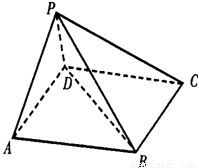
.
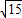 ,PD=
,PD=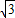 .
.
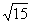 ,PD=
,PD=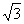 。
。