题目内容
(本小题满分12分)
已知向量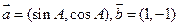 ,且
,且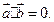
(Ⅰ)求tanA的值;
(Ⅱ)求函数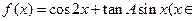 R)的值域.
R)的值域.
已知向量
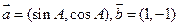 ,且
,且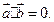
(Ⅰ)求tanA的值;
(Ⅱ)求函数
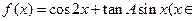 R)的值域.
R)的值域.tanA=1,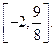
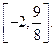
(Ⅰ)由题意得
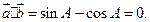 ························· 2分
························· 2分
因为cosA≠0, ···························· 3分
所以tanA="1." ····························· 4分
(Ⅱ)由(Ⅰ)知tanA=1得
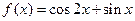 ······················· 5分
······················· 5分
=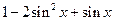 ························ 6分
························ 6分
=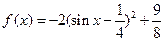 ····················· 7分
····················· 7分
因为x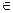 R,所以
R,所以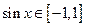 .······················ 8分
.······················ 8分
当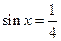 时,f(x)有最大值
时,f(x)有最大值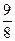 ,··················· 10分
,··················· 10分
当sinx=-1时,f(x)有最小值-2,··················· 11分
所以所求函数f(x)的值域是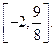 ·················· 13分
·················· 13分
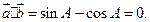 ························· 2分
························· 2分因为cosA≠0, ···························· 3分
所以tanA="1." ····························· 4分
(Ⅱ)由(Ⅰ)知tanA=1得
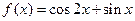 ······················· 5分
······················· 5分=
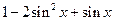 ························ 6分
························ 6分=
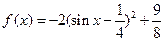 ····················· 7分
····················· 7分因为x
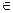 R,所以
R,所以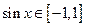 .······················ 8分
.······················ 8分当
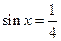 时,f(x)有最大值
时,f(x)有最大值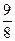 ,··················· 10分
,··················· 10分当sinx=-1时,f(x)有最小值-2,··················· 11分
所以所求函数f(x)的值域是
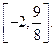 ·················· 13分
·················· 13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
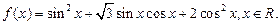
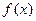 的最小正周期;
的最小正周期;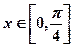 时,求函数f (x) 的最大值与最小值及相应的
时,求函数f (x) 的最大值与最小值及相应的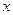 值。
值。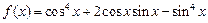 .
. 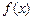 的递减区间;
的递减区间; 时,求
时,求 的集合.
的集合. ,
,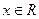
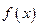 最值与最小正周期;
最值与最小正周期;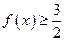
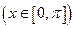 成立的
成立的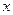 的取值范围。
的取值范围。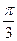 )+sin
)+sin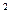 x.
x.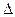 ABC的三个内角,若cosB=
ABC的三个内角,若cosB= ,
,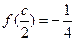 ,且C为锐角,求sinA.
,且C为锐角,求sinA.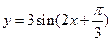 图象的对称中心是
图象的对称中心是 .
.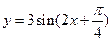 有如下命题,
有如下命题,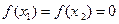 ,则
,则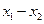 是
是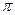 的整数倍,
的整数倍,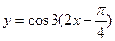 ,
,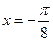 对称,
对称,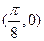 对称。其中不正确的命题是
对称。其中不正确的命题是
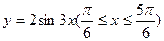 与函数y=2的图像围成一个封闭图形,这个封闭图形的面积是___
与函数y=2的图像围成一个封闭图形,这个封闭图形的面积是___ 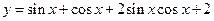 的最大值与最小值
的最大值与最小值