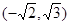题目内容
用直线y=m和直线y=x将区域x2+y2≤6分成若干块.现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是( )A.(-
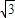 ,
,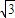 )
)B.(-
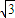 ,
,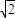 )
)C.(-
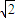 ,
,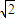 )
)D.(-
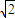 ,
,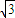 )
)
【答案】分析:区域x2+y2≤6表示以原点O(0,0)为圆心,半径等于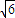 的一个圆面,经过分类讨论可得,只有当-
的一个圆面,经过分类讨论可得,只有当-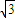 <m<
<m<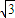 时,圆面被分成了4部分,按题中要求的涂色方法共有
时,圆面被分成了4部分,按题中要求的涂色方法共有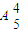 =120种,
=120种,
满足条件,从而得出结论.
解答:解:区域x2+y2≤6表示以原点O(0,0)为圆心,半径等于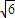 的一个圆面(圆周以及圆周内部),
的一个圆面(圆周以及圆周内部),
直线y=x和圆周的交点为 A(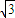 ,
,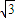 )、B(-
)、B(-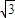 ,-
,-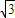 ).
).
直线y=m表示一条和x轴平行的直线,
①当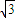 ≤|m|<
≤|m|<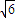 时,圆面被分成了3部分,用5种不同的颜色给这3块染色,每块只染一种颜色,且任意两块不同色,
时,圆面被分成了3部分,用5种不同的颜色给这3块染色,每块只染一种颜色,且任意两块不同色,
则共有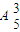 =60种不同的染色方法,不满足条件.
=60种不同的染色方法,不满足条件.
②当|m|≥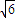 时,圆面被分成了2部分,按题中要求的涂色方法共有
时,圆面被分成了2部分,按题中要求的涂色方法共有 =20种,不满足条件.
=20种,不满足条件.
③显然,当-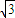 <m<
<m<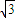 时,圆面被分成了4部分,按题中要求的涂色方法共有
时,圆面被分成了4部分,按题中要求的涂色方法共有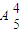 =120种,满足条件.
=120种,满足条件.
故选A.
如图所示:

点评:本题主要考查排列、组合以及简单计数原理的应用,直线和圆的位置关系,体现了数形结合及分类讨论的数学思想,属于中档题.
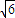 的一个圆面,经过分类讨论可得,只有当-
的一个圆面,经过分类讨论可得,只有当-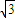 <m<
<m<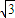 时,圆面被分成了4部分,按题中要求的涂色方法共有
时,圆面被分成了4部分,按题中要求的涂色方法共有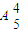 =120种,
=120种,满足条件,从而得出结论.
解答:解:区域x2+y2≤6表示以原点O(0,0)为圆心,半径等于
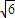 的一个圆面(圆周以及圆周内部),
的一个圆面(圆周以及圆周内部),直线y=x和圆周的交点为 A(
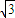 ,
,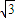 )、B(-
)、B(-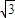 ,-
,-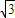 ).
).直线y=m表示一条和x轴平行的直线,
①当
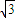 ≤|m|<
≤|m|<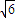 时,圆面被分成了3部分,用5种不同的颜色给这3块染色,每块只染一种颜色,且任意两块不同色,
时,圆面被分成了3部分,用5种不同的颜色给这3块染色,每块只染一种颜色,且任意两块不同色,则共有
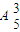 =60种不同的染色方法,不满足条件.
=60种不同的染色方法,不满足条件.②当|m|≥
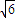 时,圆面被分成了2部分,按题中要求的涂色方法共有
时,圆面被分成了2部分,按题中要求的涂色方法共有 =20种,不满足条件.
=20种,不满足条件.③显然,当-
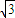 <m<
<m<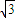 时,圆面被分成了4部分,按题中要求的涂色方法共有
时,圆面被分成了4部分,按题中要求的涂色方法共有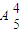 =120种,满足条件.
=120种,满足条件.故选A.
如图所示:

点评:本题主要考查排列、组合以及简单计数原理的应用,直线和圆的位置关系,体现了数形结合及分类讨论的数学思想,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
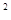 +y
+y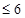 分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是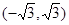
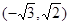

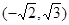
 +y
+y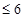 分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是
分成若干块。现在用5种不同的颜色给这若干块染色,每块只染一种颜色,且任意两块不同色,若共有120种不同的染色方法,则实数m的取值范围是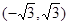 B.
B.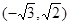 C.
C.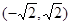 D.
D.