题目内容
把函数 的图象按向量a=(-1,2)平移得到y=f(x)的图象,则y=f(x)的定义域为
的图象按向量a=(-1,2)平移得到y=f(x)的图象,则y=f(x)的定义域为
- A.{x|x≥-1}
- B.{x|x≥0}
- C.{x|x≥0}∪{-1}
- D.{x|-1≤x≤0}
D
分析:由题设知y=f(x)的解析式为: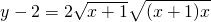 ,即
,即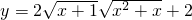 ,其定义域为
,其定义域为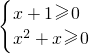 ,由此能求出结果.
,由此能求出结果.
解答:∵函数 的图象按向量a=(-1,2)平移得到y=f(x)的图象,
的图象按向量a=(-1,2)平移得到y=f(x)的图象,
∴y=f(x)的解析式为: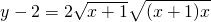 ,
,
即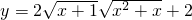 ,
,
其定义域为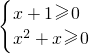 ,
,
解得{x|-1≤x≤0}.
故答案为:{x|-1≤x≤0}.
点评:本题考查函数的定义域及其求法,解题时要认真审题,注意平移变换的灵活运用.
分析:由题设知y=f(x)的解析式为:
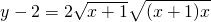 ,即
,即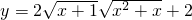 ,其定义域为
,其定义域为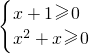 ,由此能求出结果.
,由此能求出结果.解答:∵函数
 的图象按向量a=(-1,2)平移得到y=f(x)的图象,
的图象按向量a=(-1,2)平移得到y=f(x)的图象,∴y=f(x)的解析式为:
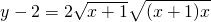 ,
,即
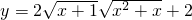 ,
,其定义域为
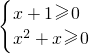 ,
,解得{x|-1≤x≤0}.
故答案为:{x|-1≤x≤0}.
点评:本题考查函数的定义域及其求法,解题时要认真审题,注意平移变换的灵活运用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 的图象按向量a=(2,3)平移,得到y=f(x)的图象,则f(x)等于
的图象按向量a=(2,3)平移,得到y=f(x)的图象,则f(x)等于


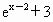

 的图象按向量a=(-1,2)平移得到y=f(x)的图象,则y=f(x)的定义域为( )
的图象按向量a=(-1,2)平移得到y=f(x)的图象,则y=f(x)的定义域为( )